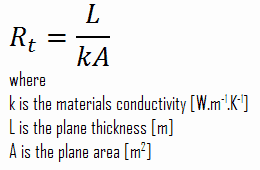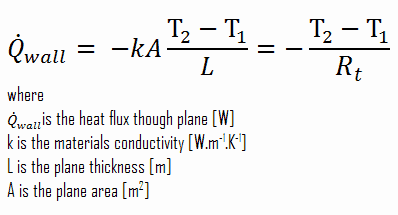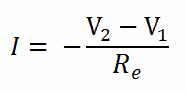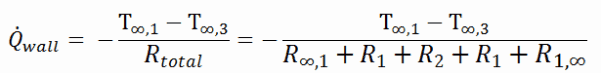Thermal Resistance – Thermal Resistivity

In engineering, another very important concept is often used. Since there is an analogy between the diffusion of heat and electrical charge, engineers often use thermal resistance (i.e., thermal resistance against heat conduction) to calculate the heat transfer through materials. Thermal resistance is the reciprocal of thermal conductance. Just as electrical resistance is associated with the conduction of electricity, thermal resistance may be associated with the conduction of heat.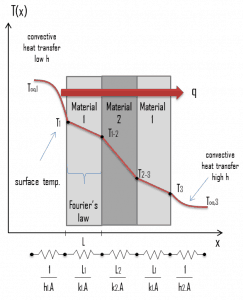

Consider a plane wall of thickness L and average thermal conductivity k. The two surfaces of the wall are maintained at constant temperatures of T₁ and T₂. For one-dimensional steady heat conduction through the wall, we have T(x). Then Fourier’s law of heat conduction for the wall can be expressed as:

Definition of Thermal Resistance

Thermal resistance is a heat property and a temperature difference measurement by which an object or material resists a heat flow. The thermal resistance for conduction in a plane wall is defined as:

Since the concept of thermal resistance can be used in a variety of engineering branches, we define:

• Absolute thermal resistance, R_t, which has units of [K/W]. Absolute thermal resistance is a property of a particular component, which has defined geometry (thickness – L, area – A, and shape). For example, a characteristic of a defined heat exchanger. Only a temperature difference is needed to solve for heat transfer.
• The specific thermal resistance or specific thermal resistivity, R_λ, has units of [(K·m)/W]. Specific thermal is a material constant, and material thickness and a temperature difference are required to solve for heat transfer.
• R-value. R-value (thermal insulance factor) is a measure of thermal resistance. The higher the R-value, the greater the insulating effectiveness. Thermal insulance has the units [(m².K)/W] in SI units or [(ft²·°F·hr)/Btu] in imperial units. It is the thermal resistance of the unit area of a material. The R-value depends on the type of insulation, its thickness, and its density. An area and a temperature difference are required to solve for heat transfer.

The analogy to Electric Resistance

The equation above for heat flow is analogous to the relation for electric current flow I, expressed as:

where R_e = L/σ_eA is the electric resistance and V₁ – V₂ is the voltage difference across the resistance (σ_e is the electrical conductivity). The analogy between both equations is obvious. The rate of heat transfer through a layer corresponds to the electric current, the thermal resistance corresponds to electrical resistance, and the temperature difference corresponds to the voltage difference across the layer. The temperature difference is the potential or driving function for the heat flow, resulting in the Fourier equation being written in a form similar to Ohm’s Law of Electrical Circuit Theory.

Circuit representations provide a useful tool for conceptualizing and quantifying heat transfer problems. This analogy can also be used for the thermal resistance of the surface against heat convection. Note that when the convection heat transfer coefficient is very large (h → infinity), the convection resistance becomes zero and the surface temperature approaches the bulk temperature. This situation is approached in practice at surfaces where intensive boiling and condensation occur.

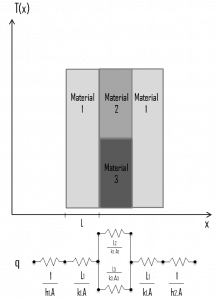
The heat transfer through the composite wall can be calculated from these resistances. The rate of steady heat transfer between two surfaces is equal to the temperature difference divided by the total thermal resistance between those two surfaces.

The equivalent thermal circuit for the plane wall with convection surface conditions is shown in the figure.

Thermal Contact Resistance – Thermal Contact Conductance

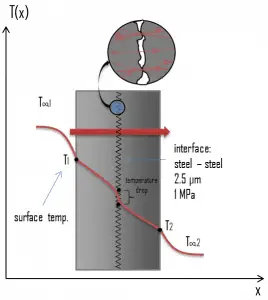In thermal engineering, the thermal contact conductance [W/m².K] or thermal contact resistance [m².K/W] represents the heat conduction between two solid bodies. When components are bolted or otherwise pressed together, a knowledge of the thermal performance of such joints is also needed. The temperature drop across the interface between materials may be appreciable in these composite systems. This temperature drop is characterized by the thermal contact conductance coefficient, h_c, which indicates the thermal conductivity, or ability to conduct heat, between two bodies in contact. While extensive databases exist on the thermal properties of bulk materials, similar databases for pressed contacts do not.

The inverse of this property is termed thermal contact resistance.

The contact resistance depends on the surface roughness greatly, and the pressure holding the two surfaces together also influences the contact resistance. Thermal contact resistance decreases with decreasing surface roughness and increasing interface pressure. This is attributed to the fact that the contact surface between the bodies grows as the contact pressure grows. When two such surfaces are pressed against each other, the peaks will form good material contact, but the valleys will form voids filled with air. These voids filled with air act as insulation because of the low thermal conductivity of air. The limited number and size of the contact spots result in an actual contact area that is significantly smaller than the apparent contact area. In the case of metallic composite material, which is placed in a vacuum, thermal conduction through the contact spots is the primary mode of heat transfer. The contact resistance is generally greater than when the composite material is in the presence of air or other fluid. Moreover, thermal contact resistance is significant and may dominate for good heat conductors such as metals but can be neglected for poor heat conductors such as insulators.

For example:

• The thermal contact conductance for aluminum plates with a surface roughness of 10 μm placed in the air with the interface pressure of 1 atm is h_c = 3640 W/m².K
• The thermal contact conductance for aluminum plates with a surface roughness of 10 μm placed in helium with the interface pressure of 1 atm is h_c = 9520 W/m².K
• The thermal contact conductance for stainless steel plates with a surface roughness of 2.5 μm placed in the air with the interface pressure of 1 MPa is about h_c = 3000 W/m².K

The thermal contact resistance can be minimized by applying a thermally conducting liquid called a thermal grease such as CPU grease on the surfaces before they are pressed against each other. The main role of thermal grease is to eliminate air gaps or spaces (which act as a thermal insulator) from the interface area to maximize heat transfer. The thermal conductivity of the interstitial material and its pressure are the two properties governing its influence on contact conductance.

Special Reference: Madhusudana, Chakravarti V., Thermal Contact Conductance. Springer International Publishing, 2014. ISBN: 978-3-319-01276-6.