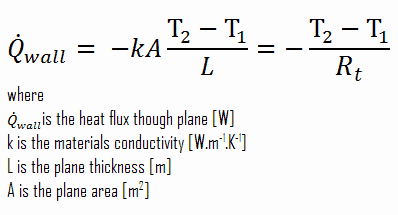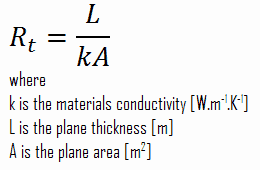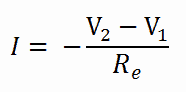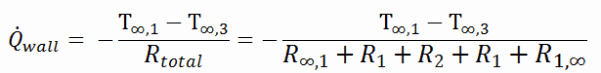Facebook Instagram Youtube Twitter

Thermal Resistance – Analogy to Electric Resistance

Thermal Resistance – Thermal Resistivity

thermal resistance - definition - analogyIn engineering, another very important concept is often used. Since there is an analogy between the diffusion of heat and electrical charge, engineers often use thermal resistance (i.e., thermal resistance against heat conduction) to calculate the heat transfer through materials. Thermal resistance is the reciprocal of thermal conductance. Just as electrical resistance is associated with the conduction of electricity, thermal resistance may be associated with the conduction of heat.

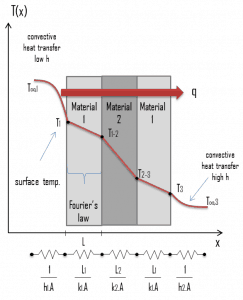
Consider a plane wall of thickness L and average thermal conductivity k. The two surfaces of the wall are maintained at constant temperatures of T1 and T2. For one-dimensional steady heat conduction through the wall, we have T(x). Then Fourier’s law of heat conduction for the wall can be expressed as:

Fourier’s law with thermal resistance

Definition of Thermal Resistance

Thermal resistance is a heat property and a temperature difference measurement by which an object or material resists a heat flow. The thermal resistance for conduction in a plane wall is defined as:

thermal resistance - definition

Since the concept of thermal resistance can be used in a variety of engineering branches, we define:

  • Absolute thermal resistance, Rt, which has units of [K/W]. Absolute thermal resistance is a property of a particular component, which has defined geometry (thickness – L, area – A, and shape). For example, a characteristic of a defined heat exchanger. Only a temperature difference is needed to solve for heat transfer.
  • The specific thermal resistance or specific thermal resistivity, Rλ, has units of [(K·m)/W]. Specific thermal is a material constant, and material thickness and a temperature difference are required to solve for heat transfer.
  • R-value. R-value (thermal insulance factor) is a measure of thermal resistance. The higher the R-value, the greater the insulating effectiveness. Thermal insulance has the units [(m2.K)/W] in SI units or [(ft2·°F·hr)/Btu] in imperial units. It is the thermal resistance of the unit area of a material. The R-value depends on the type of insulation, its thickness, and its density. An area and a temperature difference are required to solve for heat transfer.

The analogy to Electric Resistance

The equation above for heat flow is analogous to the relation for electric current flow I, expressed as:

analogy to electric resistance

where Re = L/σeA is the electric resistance and V1 – V2 is the voltage difference across the resistance (σe is the electrical conductivity). The analogy between both equations is obvious. The heat transfer rate through a layer corresponds to the electric current, thermal resistance corresponds to electrical resistance, and temperature difference corresponds to the voltage difference across the layer. The temperature difference is the potential or driving function for the heat flow, resulting in the Fourier equation being written similarly to Ohm’s Law of Electrical Circuit Theory.

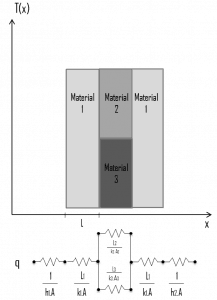thermal resistance - composite wallsCircuit representations provide a useful tool for conceptualizing and quantifying heat transfer problems. This analogy can also be used for the thermal resistance of the surface against heat convection. Note that when the convection heat transfer coefficient is very large (h → infinity), the convection resistance becomes zero and the surface temperature approaches the bulk temperature. This situation is approached in practice at surfaces where intensive boiling and condensation occur.

The heat transfer through the composite wall can be calculated from these resistances. The rate of steady heat transfer between two surfaces is equal to the temperature difference divided by the total thermal resistance between those two surfaces.

thermal resistance - equation

The equivalent thermal circuit for the plane wall with convection surface conditions is shown in the figure.

See also: Wiedemann–Franz Law

 
References:
Heat Transfer:
  1. Fundamentals of Heat and Mass Transfer, 7th Edition. Theodore L. Bergman, Adrienne S. Lavine, Frank P. Incropera. John Wiley & Sons, Incorporated, 2011. ISBN: 9781118137253.
  2. Heat and Mass Transfer. Yunus A. Cengel. McGraw-Hill Education, 2011. ISBN: 9780071077866.
  3. Fundamentals of Heat and Mass Transfer. C. P. Kothandaraman. New Age International, 2006, ISBN: 9788122417722.
  4. U.S. Department of Energy, Thermodynamics, Heat Transfer and Fluid Flow. DOE Fundamentals Handbook, Volume 2 of 3. May 2016.

Nuclear and Reactor Physics:

  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
  9. Paul Reuss, Neutron Physics. EDP Sciences, 2008. ISBN: 978-2759800414.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2. 
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See above:

Thermal Resistivity