Facebook Instagram Youtube Twitter

Critical Point of Water

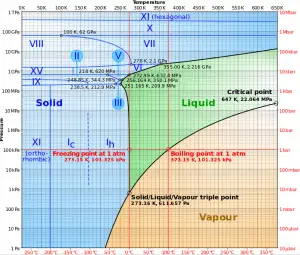
In thermodynamics, a critical point (or critical state) is the endpoint of a phase equilibrium curve. The phase diagram of water is a pressure-temperature diagram for water that shows how all three phases (solid, liquid, and vapor) may coexist together in thermal equilibrium. Along the vaporization line, the liquid and vapor phases are in equilibrium. The solid and liquid phases are in equilibrium along the fusion line, and along the sublimation line, the solid and vapor phases are in equilibrium. The only point at which all three phases may exist in equilibrium is the triple point. The vaporization line ends at the critical point because there is no distinct change from the liquid to the vapor phase above the critical point.

Above the critical point, there is no constant-temperature vaporization process. At the critical point the saturated-liquid and saturated-vapor states are identical. The temperature, pressure, and specific volume at the critical point are called the critical temperature, critical pressure, and critical volume. For water, these parameters are the following:

Parameters of Critical Point

  • Pcr = 22.09 MPa
  • Tcr = 374.14 °C (or 647.3 K)
  • vcr = 0.003155 m3/kg
  • uf = ug = 2014 kJ/kg
  • hf = hg = 2084 kJ/kg
  • sf = sg =4.406 kJ/kg K
Phase diagram of water
Phase diagram of water.
Source: wikipedia.org CC BY-SA
  • Pcr = 22.09 MPa
  • Tcr = 374.14 °C (or 647.3 K)
  • vcr = 0.003155 m3/kg
  • uf = ug = 2014 kJ/kg
  • hf = hg = 2084 kJ/kg
  • sf = sg =4.406 kJ/kg K

A supercritical phase (e.g.,, water at a pressure above the critical pressure) does not separate into two phases when cooled at constant pressure (along a horizontal line above the critical point in the phase diagram). Instead, its properties change gradually and continuously from those we ordinarily associate with a gas (low density, large compressibility) to those of a liquid (high density, small compressibility) without a phase change.

As can be seen from steam tables, as we approach the critical point, the differences in physical properties (such as density and enthalpy) between the liquid and vapor phases become smaller. For example, below the critical point at the pressure of 21.8 MPa and the temperature of 373°C, the specific enthalpy of saturated liquid is 1970 kJ/kg, while the specific enthalpy of saturated vapor is 2230 kJ/kg. The specific heat of vaporization is only 260 kJ/kg. Exactly at the critical point, these differences become zero, and at this point, the distinction between liquid and vapor disappears. The heat of vaporization also becomes zero at the critical point.

Near the critical point, the physical properties of the liquid and the vapor change dramatically. For example, liquid water under normal conditions has a low thermal expansion coefficient, is nearly incompressible, is an excellent solvent for electrolytes, and has a high dielectric constant. But near the critical point, all these properties change into the exact opposite: water becomes compressible, has a significant thermal expansion coefficient, has a low dielectric constant, is a bad solvent for electrolytes. At pressures greater than the critical pressure, the physical properties undergo a fast transition but without singularities. With a further increase in pressure, the transition becomes smoother. This transition region is called the pseudocritical region. At a given pressure, the temperature where the specific heat has its maximum is called pseudocritical point.

Critical Point
For nearly all familiar materials, the critical pressures are much greater than atmospheric pressure. Therefore we don’t observe this behavior in everyday life.

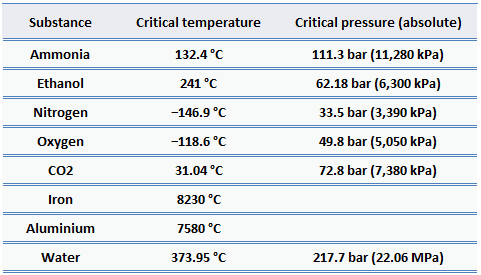
For nearly all familiar materials, the critical pressures are much greater than atmospheric pressure. Therefore we don’t observe this behavior in everyday life. But in energy engineering, there are many applications for supercritical water. One of the ways to increase the thermal efficiency of thermodynamic cycles (e.g.,, Rankine cycle) is to increase the peak temperature and pressure in the boiler. High-pressure steam boilers in thermal power plants regularly run at pressures and temperatures well above the critical point.

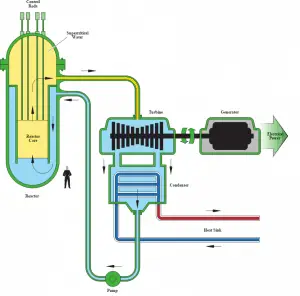
Concept of the SCWR
Concept of the SCWR.
Author (Public domain): U.S. Department of Energy

In nuclear engineering, the supercritical water reactor is considered a promising advancement for nuclear power plants because of its high thermal efficiency (~45 % vs. ~33 % for current LWRs). This reactor concept operates at supercritical pressure (i.e., greater than 22.1 MPa) and belongs to Generation IV reactor designs.

See also: Supercritical Water Reactor

 
References:
Reactor Physics and Thermal Hydraulics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. Todreas Neil E., Kazimi Mujid S. Nuclear Systems Volume I: Thermal Hydraulic Fundamentals, Second Edition. CRC Press; 2 edition, 2012, ISBN: 978-0415802871
  6. Zohuri B., McDaniel P. Thermodynamics in Nuclear Power Plant Systems. Springer; 2015, ISBN: 978-3-319-13419-2
  7. Moran Michal J., Shapiro Howard N. Fundamentals of Engineering Thermodynamics, Fifth Edition, John Wiley & Sons, 2006, ISBN: 978-0-470-03037-0
  8. Kleinstreuer C. Modern Fluid Dynamics. Springer, 2010, ISBN 978-1-4020-8670-0.
  9. U.S. Department of Energy, THERMODYNAMICS, HEAT TRANSFER, AND FLUID FLOW. DOE Fundamentals Handbook, Volume 1, 2, and 3. June 1992.

See above:

Water