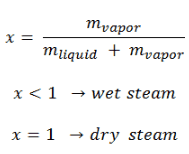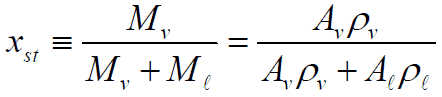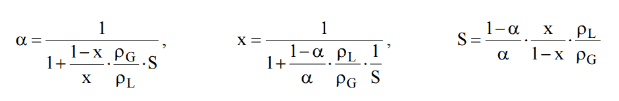See also: Properties of Steam
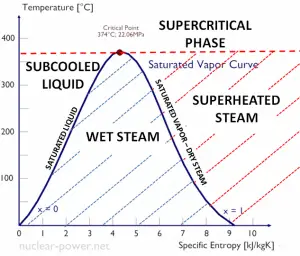
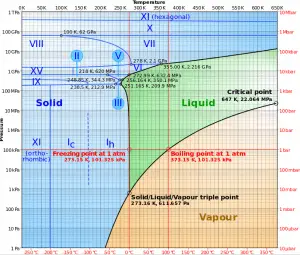
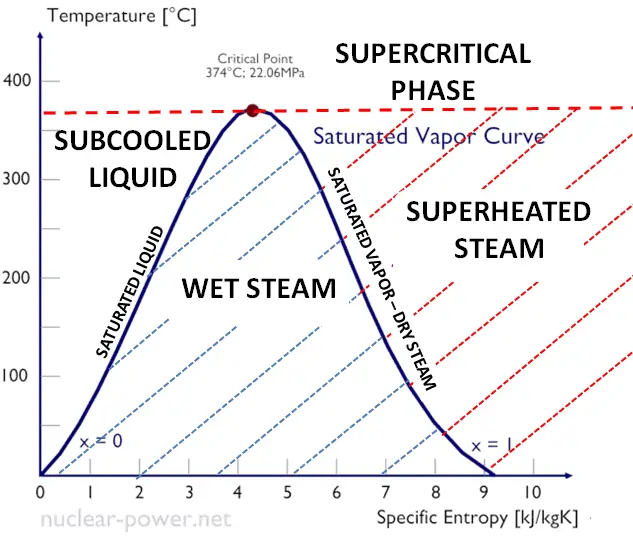
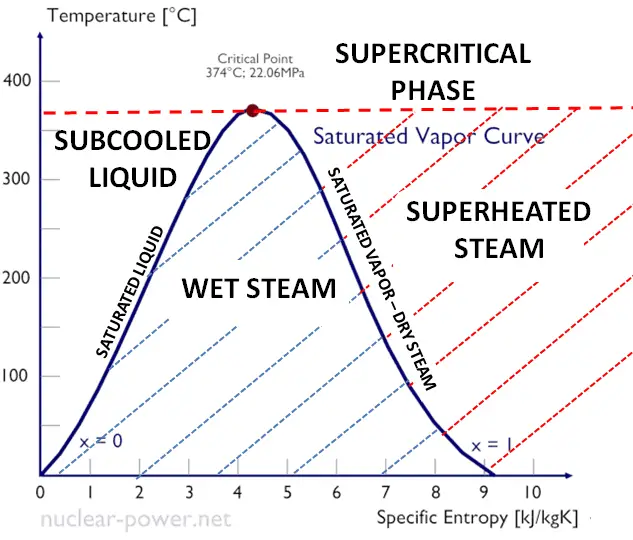
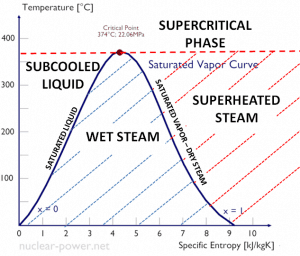
As seen from the phase diagram of water, in the two-phase regions (e.g.,, on the border of vapor/liquid phases), specifying temperature alone will set the pressure, and specifying pressure will set the temperature. But these parameters will not define the volume and enthalpy because we will need to know the relative proportion of the two phases present.
The mass fraction of the vapor in a two-phase liquid-vapor region is called the vapor quality (or dryness fraction), x, and it is given by the following formula:
The value of the quality ranges from zero to unity. Although defined as a ratio, the quality is frequently given as a percentage. From this point of view, we distinguish between three basic types of steam. It must be added, at x=0, we are talking about the saturated liquid state (single-phase).
This classification of steam has its limitation. Consider the system’s behavior which is heated at a pressure that is higher than the critical pressure. In this case, there would be no change in phase from liquid to steam. In all states, there would be only one phase. Vaporization and condensation can occur only when the pressure is less than the critical pressure. The terms liquid and vapor tend to lose their significance.
See also: Saturation.
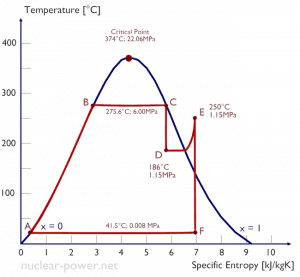
See also: Throttling of Steam
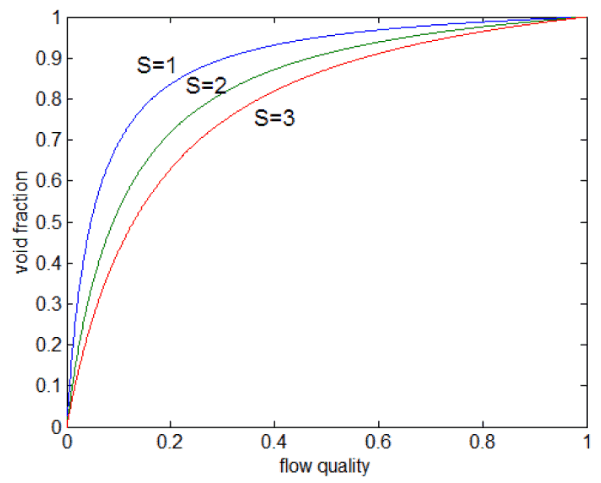
Static Quality vs. Flow Quality
See also: Two-phase Fluid Flow
In this section we will consider the simultaneous flow of gas (or vapor) and liquid water (as encountered in steam generators and condensers) in concurrent flow through a duct with cross-sectional area A. The subscripts “v” and “ℓ” indicate the vapor and liquid phase, respectively. Fundamental parameters that characterize this flow are:
Flow Quality
In two-phase fluid flow in is convenient to use the flow quality instead of the static quality. The flow quality in a two-phase fluid flow is defined as:
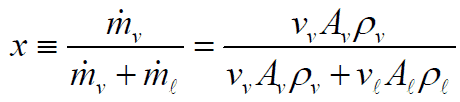
The relations between x, α, and S can be deducted, and the result is: