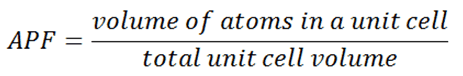Some of the properties of crystalline solids depend on the crystal structure of the material and how atoms, ions, or molecules are spatially arranged. A crystal lattice is a repeating pattern of mathematical points that extends throughout space, and the forces of chemical bonding cause this repetition. This repeated pattern controls properties like strength, ductility, density, conductivity (property of conducting or transmitting heat, electricity, etc.), and shape. There are 14 general types of such patterns known as Bravais lattices.
Three relatively simple crystal structures are found for most of the common metals:
-
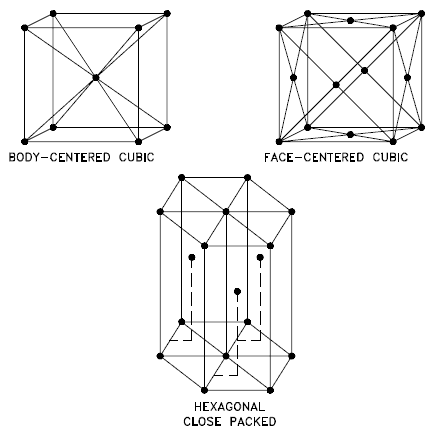
Source: U.S. Department of Energy, Material Science. DOE Fundamentals Handbook, Volume 1 and 2. January 1993. Body-centered Cubic – bcc. In a body-centered cubic (bcc) arrangement of atoms, the unit cell consists of eight atoms at the corners of a cube and one atom at the body center of the cube. In a bcc arrangement, a unit cell contains (8 corner atoms × ⅛) + (1 center atom × 1) = 2 atoms. The packing is more efficient (68%) than simple cubic, and the structure is common for alkali and early transition metals. Metals containing BCC structures include ferrite, chromium, vanadium, molybdenum, and tungsten. These metals possess high strength and low ductility.
- Face-centered Cubic – fcc. In a face-centered cubic (fcc) arrangement of atoms, the unit cell consists of eight atoms at the corners of a cube and one atom at the center of each of the faces of the cube. In an fcc arrangement, a unit cell contains (8 corner atoms × ⅛) + (6 face atoms × ½) = 4 atoms. This structure, along with its hexagonal relative (hcp), has the most efficient packing (74%). Metals containing FCC structures include austenite, aluminum, copper, lead, silver, gold, nickel, platinum, and thorium. These metals possess low strength and high ductility.
- Hexagonal Close-packed – hcp. In a hexagonal close-packed (hcp) arrangement of atoms, the unit cell consists of three layers of atoms. The top and bottom layers contain six atoms at the corners of a hexagon and one atom at the center of each hexagon. The middle layer contains three atoms nestled between the atoms of the top and bottom layers. Hence, the name is close-packed. Hexagonal close-packed (hcp) is one of the two simple types of atomic packing with the highest density, the other being the face-centered cubic (fcc). However, unlike the fcc, it is not a Bravais lattice as there are two nonequivalent sets of lattice points. Metals containing HCP structures include beryllium, magnesium, zinc, cadmium, cobalt, thallium, and zirconium. HCP metals are not as ductile as FCC metals.
Atomic Packing Factor – APF
In crystallography, atomic packing factor (APF), packing efficiency, or packing fraction is the sum of the sphere volumes of all atoms within a unit cell (assuming the atomic hard-sphere model) divided by the unit cell volume.
By convention, the APF is determined by assuming that atoms are rigid spheres, and the radius of the spheres is taken to be the maximum value such that the atoms do not overlap. In materials science, the atomic packing factor of a unit cell explains many properties of materials. For example, metals with a high atomic packing factor will have a higher malleability or ductility, similar to how a road is smoother when the stones are closer together, allowing metal atoms to slide past one another more easily.
For example, in an fcc arrangement, a unit cell contains (8 corner atoms × ⅛) + (6 face atoms × ½) = 4 atoms. This structure, along with its hexagonal relative (hcp), has the most efficient packing (74%).