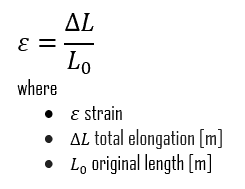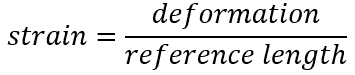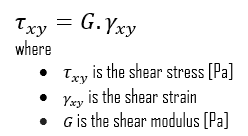 In the mechanics of materials, the strength of a material is its ability to withstand an applied load without failure or plastic deformation. The strength of materials considers the relationship between the external loads applied to a material and the resulting deformation or change in material dimensions. In designing structures and machines, it is important to consider these factors so that the material selected will have adequate strength to resist applied loads or forces and retain its original shape. The strength of a material is its ability to withstand this applied load without failure or plastic deformation.
In the mechanics of materials, the strength of a material is its ability to withstand an applied load without failure or plastic deformation. The strength of materials considers the relationship between the external loads applied to a material and the resulting deformation or change in material dimensions. In designing structures and machines, it is important to consider these factors so that the material selected will have adequate strength to resist applied loads or forces and retain its original shape. The strength of a material is its ability to withstand this applied load without failure or plastic deformation.
However, we must note that the load which will deform a small component will be less than the load to deform a larger component of the same material. Therefore, the load (force) is not a suitable term for strength. Instead, we can use the force (load) per unit of area (σ = F/A), called stress, which is constant (until deformation occurs) for a given material regardless of the size of the component part. In this concept, strain is also a very important variable since it defines the deformation of an object. In summary, the mechanical behavior of solids is usually defined by constitutive stress-strain relations. A deformation is called elastic deformation if the stress is a linear function of strain. In other words, stress and strain follow Hooke’s law. Beyond the linear region, stress and strain show nonlinear behavior. This inelastic behavior is called plastic deformation.
Stress
In mechanics and materials science, stress (represented by a lowercase Greek letter sigma – σ) is a physical quantity that expresses the internal forces that neighboring particles of a continuous material exert on each other. At the same time, strain is the measure of the deformation of the material, which is not a physical quantity.
Although it is impossible to measure the intensity of this stress, the external load and the area to which it is applied can be measured. Stress (σ) can be equated to the load per unit area or the force (F) applied per cross-sectional area (A) perpendicular to the force as:
When a metal is subjected to a load (force), it is distorted or deformed, no matter how strong the metal or light the load. If the load is small, the distortion will probably disappear when the load is removed. The intensity, or degree, of distortion, is known as strain. A deformation is called elastic deformation if the stress is a linear function of strain. In other words, stress and strain follow Hooke’s law. Beyond the linear region, stress and strain show nonlinear behavior. This inelastic behavior is called plastic deformation.
Stress is the internal resistance, or counterforce, of a material to the distorting effects of an external force or load. These counterforces tend to return the atoms to their normal positions. The total resistance developed is equal to the external load.
Types of Stress
Stresses occur in any material subject to a load or applied force. There are many types of stress, but they can all be generally classified into one of six categories:
- Structural stresses are stresses produced in structural members because of the weights they support. The weights provide the loadings. These stresses are found in building foundations and frameworks, as well as in machinery parts.
- Residual stresses are stresses caused by manufacturing processes. This type of stress remains in a solid material after the original cause of the stress has been removed. For example, welding leaves residual stresses in the metals welded. The heat from welding may cause localized expansion, which is taken up during welding by either the molten metal or the placement of parts being welded.
- Pressure stresses are stresses induced in vessels containing pressurized materials, and the loading is provided by the same force producing the pressure. The reactor vessel is a prime example of a pressure vessel in a reactor facility. One safety issue that is a long-term problem brought on by the aging of nuclear facilities is pressurized thermal shock (PTS). PTS is the shock experienced by a thick-walled vessel due to the combined stresses from a rapid temperature and/or pressure change.
- Thermal stresses exist whenever temperature gradients are present in a material, and different temperatures produce different expansions and subject materials to internal stress. This type of stress is particularly noticeable in mechanisms operating at high temperatures cooled by a cold fluid. One safety issue that is a long-term problem brought on by the aging of nuclear facilities is pressurized thermal shock (PTS). PTS is the shock experienced by a thick-walled vessel due to the combined stresses from a rapid temperature and/or pressure change.
- Flow stresses occur when a mass of flowing fluid induces dynamic pressure on a conduit wall. The force of the fluid striking the wall acts as the load. This type of stress may be applied in an unsteady fashion when flow rates fluctuate. Water hammer is an example of transient flow stress. A Water hammer in a pipe or tube is a pressure spike caused by a sudden flow rate variation. And velocity energy is converted to pressure energy.
- Fatigue stresses. Fatigue is the weakening of a material caused by cyclic loading that results in progressive and localized structural damage and the growth of cracks. Once a crack has been initiated, each loading cycle will grow the crack a small amount. The stresses could be due to vibration or thermal cycling.
Applied Stress
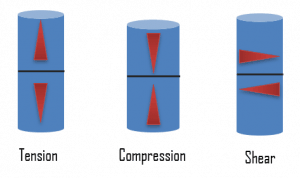 From an internal point of view, stress intensity within the body of a component is expressed as one of three basic internal load types: tension, compression, and shear. In engineering practice, many loads are torsional rather than pure shear. Mathematically, there are only two types of an internal load because tensile and compressive stress may be regarded as the positive and negative versions of the same type of normal loading.
From an internal point of view, stress intensity within the body of a component is expressed as one of three basic internal load types: tension, compression, and shear. In engineering practice, many loads are torsional rather than pure shear. Mathematically, there are only two types of an internal load because tensile and compressive stress may be regarded as the positive and negative versions of the same type of normal loading.
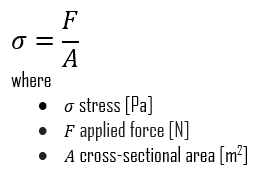 Tensile stress. One of the most common mechanical stress-strain tests is performed in tension. Tensile stress is that type of stress in which the two sections of material on either side of a stress plane tend to pull apart or elongate. The capacity of a material or structure to withstand loads tending to elongate is known as ultimate tensile strength (UTS). Ultimate tensile strength is measured by the maximum stress a material can withstand while being stretched or pulled before breaking. In the study of the strength of materials, tensile strength, compressive strength, and shear strength can be analyzed independently. Because tensile and compressive loads produce stresses that act across a plane in a direction perpendicular (normal) to the plane, tensile and compressive stresses are called normal stresses.
Tensile stress. One of the most common mechanical stress-strain tests is performed in tension. Tensile stress is that type of stress in which the two sections of material on either side of a stress plane tend to pull apart or elongate. The capacity of a material or structure to withstand loads tending to elongate is known as ultimate tensile strength (UTS). Ultimate tensile strength is measured by the maximum stress a material can withstand while being stretched or pulled before breaking. In the study of the strength of materials, tensile strength, compressive strength, and shear strength can be analyzed independently. Because tensile and compressive loads produce stresses that act across a plane in a direction perpendicular (normal) to the plane, tensile and compressive stresses are called normal stresses.- Compressive stress. Compressive stress is the reverse of tensile stress. Adjacent parts of the material tend to press against each other through a typical stress plane. Compressive stress to bars, columns, etc., leads to shortening. Compressive stress is defined similarly to tensile stress, but it has negative values to express the compression since delta L has the opposite direction. One can increase the compressive stress until compressive strength is reached. Then materials will react with ductile behavior or with a fracture in the case of brittle materials. Because tensile and compressive loads produce stresses that act across a plane in a direction perpendicular (normal) to the plane, tensile and compressive stresses are called normal stresses. The ability of a material to react to compressive stress or pressure is called compressibility.
 Shear stress. Shear stress exists when two parts of material tend to slide across each other in any typical plane of shear upon application of force parallel to that plane. Torsion is a variation of pure shear in which a structural member is twisted. Torsional forces produce a rotational motion about the longitudinal axis of one end of the member relative to the other. Shear stress is also of great importance in nature, intimately related to the downslope movement of earth materials (as in the case of avalanches).
Shear stress. Shear stress exists when two parts of material tend to slide across each other in any typical plane of shear upon application of force parallel to that plane. Torsion is a variation of pure shear in which a structural member is twisted. Torsional forces produce a rotational motion about the longitudinal axis of one end of the member relative to the other. Shear stress is also of great importance in nature, intimately related to the downslope movement of earth materials (as in the case of avalanches).
Strain
In materials science, strain is also a very important variable since it defines the deformation of an object. Unlike stress in an object, which you can’t see, deformation is a visible and measurable quantity. When you pull on a tension rod, you can see the rod physically increase in length (or elongate). When you bend a beam, you see it curve. Deformations are a direct indicator of strain. The mechanical behavior of solids is usually defined by constitutive stress-strain relations. When a metal is subjected to a load (force), it is distorted or deformed, no matter how strong the metal or light the load. If the load is small, the distortion will probably disappear when the load is removed. Such a proportional dimensional change (intensity or degree of the distortion) is called strain. Due to applied stress, it is measured as the material’s total deformation (elongation) per reference length.
In the mechanics of materials, we can define two basic types of strain:
- Normal strains. A normal strain results from tensile stress and is a strain computed from relative displacements that are measured perpendicular to two reference planes. Normal strains measure the relative perpendicular movement of one reference plane for another. The symbol for normal strain is usually the lowercase Greek symbol epsilon (ε).
- Shear strains. A shear strain results from shear stress, and it is a strain computed from relative displacements that are measured parallel to two reference planes. Shear strains measure the relative parallel movement of one reference plane for another. The symbol for shear strain is usually the lowercase Greek symbol gamma (γ ).
Deformation
The deformation measures how much an object deforms from its original dimensions or size in a given direction. Depending on which deformation you measure, you can calculate different types of strain.
A deformation is called elastic deformation if the stress is a linear function of strain. In other words, stress and strain follow Hooke’s law. Beyond the linear region, stress and strain show nonlinear behavior, and this inelastic behavior is called plastic deformation.
 Elastic Deformation. Elastic deformation and elastic strain is a transitory dimensional change that exists only while the initiating stress is applied and disappears immediately upon removing the stress. When a metal is subjected to a load (force), it is distorted or deformed, no matter how strong the metal or light the load. This deformation may or may not be permanent. Up to limiting stress, a body will be able to recover its dimensions on the removal of the load. The applied stresses cause the atoms in a crystal to move from their equilibrium position, and all the atoms are displaced the same amount and still maintain their relative geometry. When the stresses are removed, all the atoms return to their original positions, and no permanent deformation occurs.
Elastic Deformation. Elastic deformation and elastic strain is a transitory dimensional change that exists only while the initiating stress is applied and disappears immediately upon removing the stress. When a metal is subjected to a load (force), it is distorted or deformed, no matter how strong the metal or light the load. This deformation may or may not be permanent. Up to limiting stress, a body will be able to recover its dimensions on the removal of the load. The applied stresses cause the atoms in a crystal to move from their equilibrium position, and all the atoms are displaced the same amount and still maintain their relative geometry. When the stresses are removed, all the atoms return to their original positions, and no permanent deformation occurs.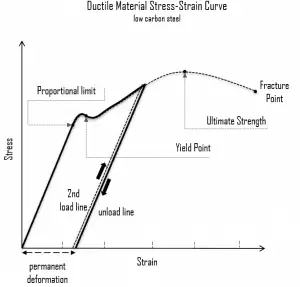 Plastic Deformation. Plastic deformation and plastic strain is a dimensional change that does not disappear when the initiating stress is removed. If the limiting load is exceeded, the body will experience permanent deformation on the removal of the load. Plastic deformation occurs in material bodies after stresses have attained a threshold value known as the elastic limit or yield stress and result from slip or dislocation mechanisms at the atomic level.
Plastic Deformation. Plastic deformation and plastic strain is a dimensional change that does not disappear when the initiating stress is removed. If the limiting load is exceeded, the body will experience permanent deformation on the removal of the load. Plastic deformation occurs in material bodies after stresses have attained a threshold value known as the elastic limit or yield stress and result from slip or dislocation mechanisms at the atomic level.
Stress-Strain Curve
 The strength of materials considers the relationship between the external loads applied to a material and the resulting deformation or change in material dimensions. In designing structures and machines, it is important to consider these factors so that the material selected will have adequate strength to resist applied loads or forces and retain its original shape. The strength of a material is its ability to withstand this applied load without failure or plastic deformation.
The strength of materials considers the relationship between the external loads applied to a material and the resulting deformation or change in material dimensions. In designing structures and machines, it is important to consider these factors so that the material selected will have adequate strength to resist applied loads or forces and retain its original shape. The strength of a material is its ability to withstand this applied load without failure or plastic deformation.
However, we must note that the load which will deform a small component will be less than the load to deform a larger component of the same material. Therefore, the load (force) is not a suitable term for strength. Instead, we can use the force (load) per unit of area (σ = F/A), called stress, which is constant (until deformation occurs) for a given material regardless of the size of the component part. In this concept, strain is also a very important variable since it defines the deformation of an object. In summary, the mechanical behavior of solids is usually defined by constitutive stress-strain relations. A deformation is called elastic deformation if the stress is a linear function of strain. In other words, stress and strain follow Hooke’s law. Beyond the linear region, stress and strain show nonlinear behavior. This inelastic behavior is called plastic deformation.
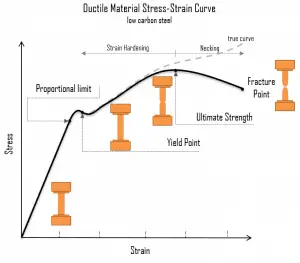
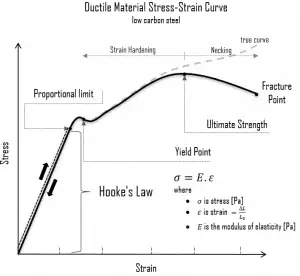
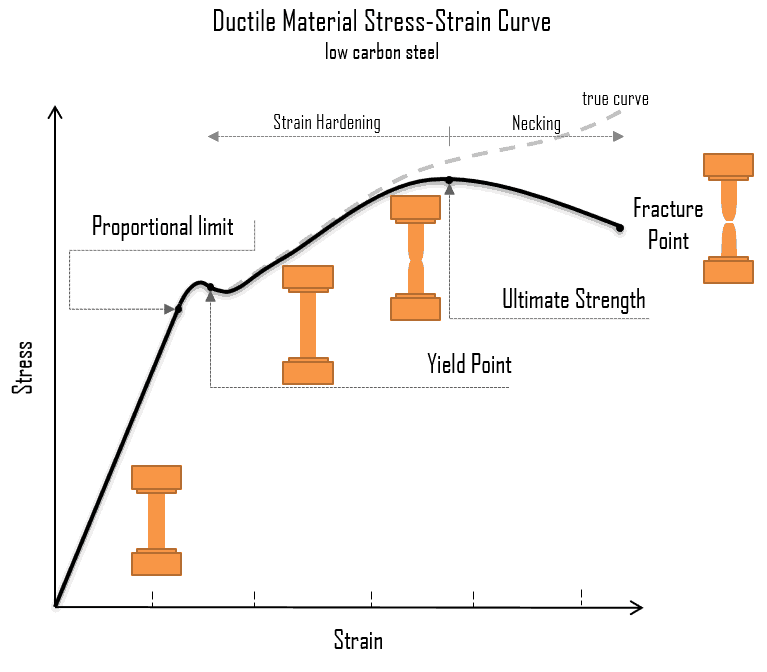
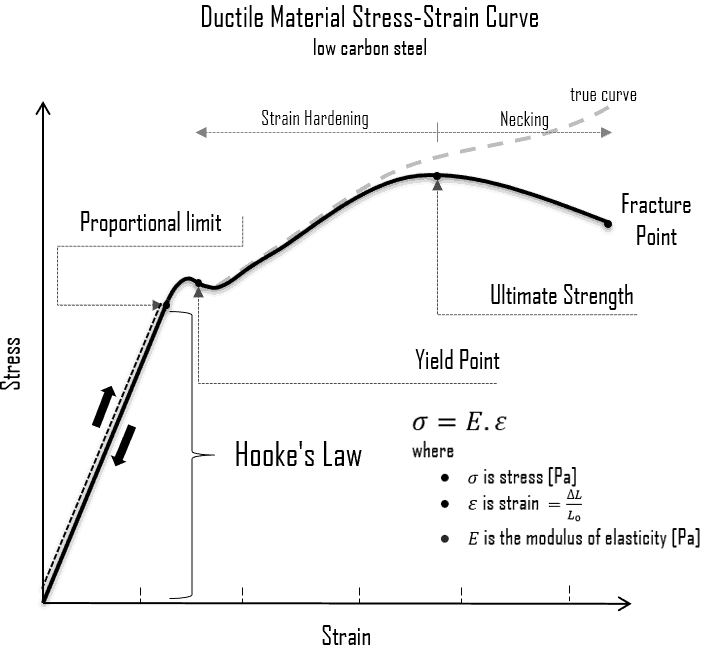
A schematic diagram for the stress-strain curve of low carbon steel at room temperature is shown in the figure. Several stages show different behaviors, which suggests different mechanical properties. Materials can miss one or more stages shown in the figure or have different stages to clarify. In this case, we have to distinguish between stress-strain characteristics of ductile and brittle materials. The following points describe the different regions of the stress-strain curve and the importance of several specific locations.
- Proportional limit. The proportional limit corresponds to the location of stress at the end of the linear region, so the stress-strain graph is a straight line, and the gradient will be equal to the elastic modulus of the material. For tensile and compressive stress, the slope of the portion of the curve where stress is proportional to strain is referred to as Young’s modulus, and Hooke’s Law applies. Between the proportional limit and the yield point, Hooke’s Law becomes questionable, and strain increases more rapidly.
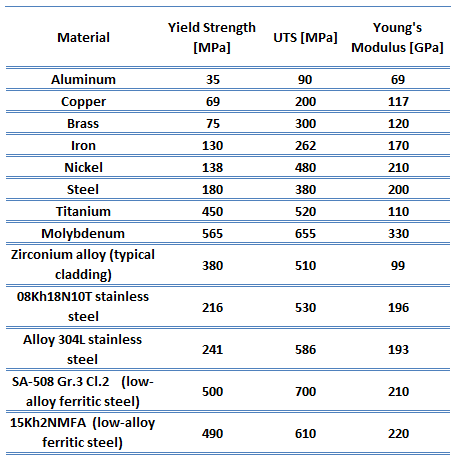
 Yield point. The yield point is the point on a stress-strain curve that indicates the limit of elastic behavior and the beginning plastic behavior. Yield strength or yield stress is the material property defined as the stress at which a material begins to deform plastically. In contrast, the yield point is where nonlinear (elastic + plastic) deformation begins. Before the yield point, the material will deform elastically and return to its original shape when the applied stress is removed. Once the yield point is passed, some fraction of the deformation will be permanent and non-reversible. Some steels and other materials exhibit a behavior termed a yield point phenomenon. Yield strengths vary from 35 MPa for low-strength aluminum to greater than 1400 MPa for high-strength steel.
Yield point. The yield point is the point on a stress-strain curve that indicates the limit of elastic behavior and the beginning plastic behavior. Yield strength or yield stress is the material property defined as the stress at which a material begins to deform plastically. In contrast, the yield point is where nonlinear (elastic + plastic) deformation begins. Before the yield point, the material will deform elastically and return to its original shape when the applied stress is removed. Once the yield point is passed, some fraction of the deformation will be permanent and non-reversible. Some steels and other materials exhibit a behavior termed a yield point phenomenon. Yield strengths vary from 35 MPa for low-strength aluminum to greater than 1400 MPa for high-strength steel.- Ultimate tensile strength. The ultimate tensile strength is the maximum on the engineering stress-strain curve. This corresponds to the maximum stress sustained by a structure in tension. Ultimate tensile strength is often shortened to “tensile strength” or “the ultimate.” If this stress is applied and maintained, a fracture will result. Often, this value is significantly more than the yield stress (as much as 50 to 60 percent more than the yield for some types of metals). When a ductile material reaches its ultimate strength, it experiences necking where the cross-sectional area reduces locally. The stress-strain curve contains no higher stress than the ultimate strength. Even though deformations can continue to increase, the stress usually decreases after achieving the ultimate strength. It is an intensive property; therefore its value does not depend on the size of the test specimen. However, it depends on other factors, such as the preparation of the specimen, the presence or otherwise of surface defects, and the temperature of the test environment and material. Ultimate tensile strengths vary from 50 MPa for aluminum to as high as 3000 MPa for very high-strength steel.
- Fracture point: The fracture point is the point of strain where the material physically separates. At this point, the strain reaches its maximum value, and the material fractures, even though the corresponding stress may be less than the ultimate strength at this point. Ductile materials have a fracture strength lower than the ultimate tensile strength (UTS), whereas, in brittle materials, the fracture strength is equivalent to the UTS. If a ductile material reaches its ultimate tensile strength in a load-controlled situation, it will continue to deform, with no additional load application, until it ruptures. However, if the loading is displacement-controlled, the deformation of the material may relieve the load, preventing rupture.
In many situations, the yield strength is used to identify the allowable stress to which a material can be subjected. This criterion is not adequate for components that have to withstand high pressures, such as those used in pressurized water reactors (PWRs). The maximum shear stress theory of failure has been incorporated into the ASME (The American Society of Mechanical Engineers) Boiler and Pressure Vessel Code, Section III, Rules for Construction of Nuclear Pressure Vessels to cover these situations. This theory states that failure of a piping component occurs when the maximum shear stress exceeds the shear stress at the yield point in a tensile test.
Ductile vs. Brittle – Stress-strain curves
Some materials break very sharply, without plastic deformation, in a brittle failure. Others, which are more ductile, including most metals, experience some plastic deformation and possibly necking before fracture. It is possible to distinguish some common characteristics among the stress-strain curves of various groups of materials. On this basis, it is possible to divide materials into two broad categories; namely:
- Ductile Materials. Ductility is the ability of a material to be elongated in tension. Ductile material will deform (elongate) more than brittle material. Ductile materials show large deformation before fracture. In ductile fracture, extensive plastic deformation (necking) takes place before fracture. Ductile fracture (shear fracture) is better than brittle fracture because there is slow propagation and an absorption of a large amount of energy before fracture. Ductility is desirable in the high temperature and high-pressure applications in reactor plants because of the added stresses on the metals. High ductility in these applications helps prevent brittle fracture.
- Brittle Materials. When subjected to stress, brittle materials break with little elastic deformation and without significant plastic deformation. Brittle materials absorb relatively little energy before fracture, even high-strength materials. In brittle fracture (transgranular cleavage), no apparent plastic deformation occurs before fracture, and cracks propagate rapidly.
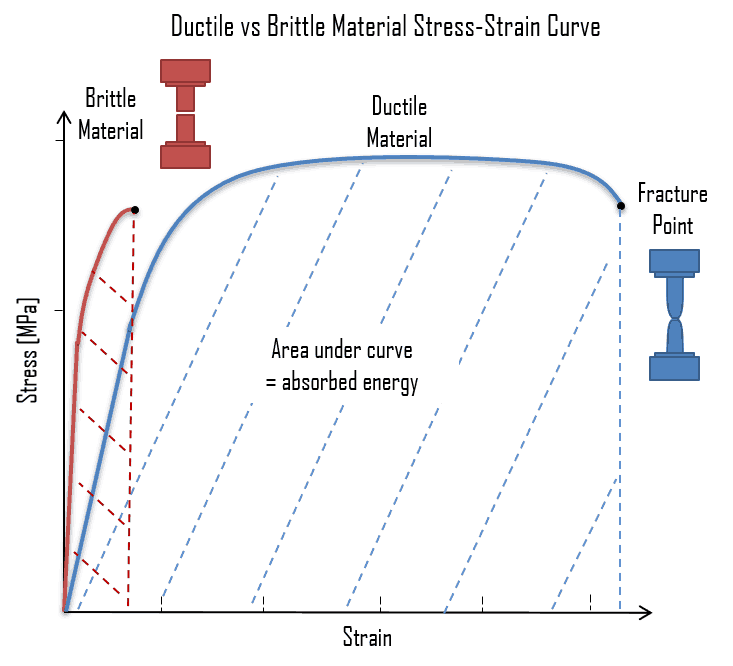 The following figure shows a typical stress-strain curve of ductile and brittle materials. Ductile material is a material with a small strength, and the plastic region is great. The material will bear more strain (deformation) before fracture. A brittle material is a material where the plastic region is small, and the strength of the material is high. The tensile test supplies three descriptive facts about a material. These are the stress at which observable plastic deformation or “yielding” begins; the ultimate tensile strength or maximum intensity of load that can be carried in tension; and the percent elongation or strain (the amount the material will stretch) and the accompanying percent reduction of the cross-sectional area caused by stretching. The rupture or fracture point can also be determined.
The following figure shows a typical stress-strain curve of ductile and brittle materials. Ductile material is a material with a small strength, and the plastic region is great. The material will bear more strain (deformation) before fracture. A brittle material is a material where the plastic region is small, and the strength of the material is high. The tensile test supplies three descriptive facts about a material. These are the stress at which observable plastic deformation or “yielding” begins; the ultimate tensile strength or maximum intensity of load that can be carried in tension; and the percent elongation or strain (the amount the material will stretch) and the accompanying percent reduction of the cross-sectional area caused by stretching. The rupture or fracture point can also be determined.
Strain Hardening
One of the stages in the stress-strain curve is the strain hardening region. This region starts as the strain goes beyond the yield point and ends at the ultimate strength point, the maximal stress shown in the stress-strain curve. In this region, the stress mainly increases as the material elongates, except that there is a nearly flat region at the beginning. Strain hardening is also called work-hardening or cold-working. It is called cold-working because the plastic deformation must occur at a temperature low enough that atoms cannot rearrange themselves. It is a process of making a metal harder and stronger through plastic deformation. When a metal is plastically deformed, dislocations move, and additional dislocations are generated. Dislocations can move if the atoms from one of the surrounding planes break their bonds and rebond with the atoms at the terminating edge. The dislocation density in a metal increases with deformation or cold work because of dislocation multiplication or the formation of new dislocations. The more dislocations within a material, the more they interact and become pinned or tangled. This will result in a decrease in the mobility of the dislocations and a strengthening of the material.
Hooke’s law
 Most polycrystalline materials have an almost constant relationship between stress and strain within their elastic range. In 1678 an English scientist named Robert Hooke ran experiments that provided data showing that strain is proportional to stress in the elastic range of material. Robert Hooke concluded that the force F in any spring is proportional to the extension (the deformation from the relaxed state) x as follows:
Most polycrystalline materials have an almost constant relationship between stress and strain within their elastic range. In 1678 an English scientist named Robert Hooke ran experiments that provided data showing that strain is proportional to stress in the elastic range of material. Robert Hooke concluded that the force F in any spring is proportional to the extension (the deformation from the relaxed state) x as follows:
F = k · x
where the term k is the stiffness of the spring and x is small compared to the total possible deformation of the spring. It must eventually fail once the forces exceed some limit since no material can be compressed beyond a certain minimum size or stretched beyond a maximum size without some permanent deformation or change of state.
In the case of tensional stress of a uniform bar (stress-strain curve), Hooke’s law describes the behavior of a bar in the elastic region. In this region, the elongation of the bar is directly proportional to the tensile force and the length of the bar and inversely proportional to the cross-sectional area and the modulus of elasticity. Up to limiting stress, a body will be able to recover its dimensions on the removal of the load. The applied stresses cause the atoms in a crystal to move from their equilibrium position, and all the atoms are displaced the same amount and still maintain their relative geometry. When the stresses are removed, all the atoms return to their original positions, and no permanent deformation occurs. According to Hooke’s law, the stress is proportional to the strain (in the elastic region), and the slope is Young’s modulus.
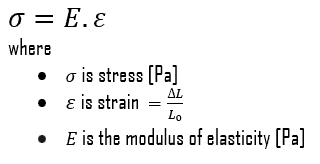 We can extend the same idea of relating stress to strain to shear applications in the linear region, relating shear stress to shear strain to create Hooke’s law for shear stress:
We can extend the same idea of relating stress to strain to shear applications in the linear region, relating shear stress to shear strain to create Hooke’s law for shear stress:
For isotropic materials within the elastic region, you can relate Poisson’s ratio (ν), Young’s modulus of elasticity (E), and the shear modulus of elasticity (G):
The elastic moduli relevant to polycrystalline materials:
 Young’s Modulus of Elasticity. Young’s modulus of elasticity is the elastic modulus for tensile and compressive stress in the linear elasticity regime of a uniaxial deformation and is usually assessed by tensile tests.
Young’s Modulus of Elasticity. Young’s modulus of elasticity is the elastic modulus for tensile and compressive stress in the linear elasticity regime of a uniaxial deformation and is usually assessed by tensile tests.- Shear Modulus of Elasticity. The shear modulus, or the modulus of rigidity, is derived from the torsion of a cylindrical test piece, describing the material’s response to shear stress. Its symbol is G. The shear modulus is one of several quantities for measuring the stiffness of materials, and it arises in the generalized Hooke’s law.
- Bulk Modulus of Elasticity. The bulk modulus of elasticity describes volumetric elasticity, or the tendency of an object to deform in all directions when uniformly loaded in all directions. For example, it describes the elastic response to hydrostatic pressure and equilateral tension (like the pressure at the bottom of the ocean or a deep swimming pool). It is also the property of a material that determines the elastic response to applying stress. For a fluid, only the bulk modulus is meaningful.