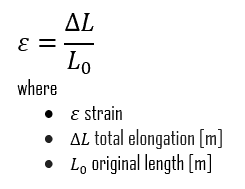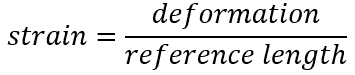In materials science, strain is also a very important variable since it defines the deformation of an object. Unlike stress in an object, which you can’t see, deformation is a visible and measurable quantity. When you pull on a tension rod, you can see the rod physically increase in length (or elongate). When you bend a beam, you see it curve. Deformations are a direct indicator of strain. The mechanical behavior of solids is usually defined by constitutive stress-strain relations. When a metal is subjected to a load (force), it is distorted or deformed, no matter how strong the metal or light the load. If the load is small, the distortion will probably disappear when the load is removed. Such a proportional dimensional change (intensity or degree of the distortion) is called strain. Due to applied stress, it is measured as the material’s total deformation (elongation) per reference length.
In the mechanics of materials, we can define two basic types of strain:
- Normal strains. A normal strain results from tensile stress and is a strain computed from relative displacements that are measured perpendicular to two reference planes. Normal strains measure the relative perpendicular movement of one reference plane for another. The symbol for normal strain is usually the lowercase Greek symbol epsilon (ε).
- Shear strains. A shear strain results from shear stress, and it is a strain computed from relative displacements that are measured parallel to two reference planes. Shear strains measure the relative parallel movement of one reference plane for another. The symbol for shear strain is usually the lowercase Greek symbol gamma (γ ).
Deformation
The deformation measures how much an object deforms from its original dimensions or size in a given direction. Depending on which deformation you measure, you can calculate different strain types.
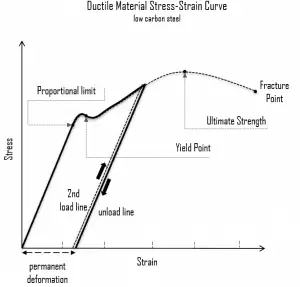
A deformation is called elastic deformation if the stress is a linear function of strain. In other words, stress and strain follow Hooke’s law. Beyond the linear region, stress and strain show nonlinear behavior, and this inelastic behavior is called plastic deformation.
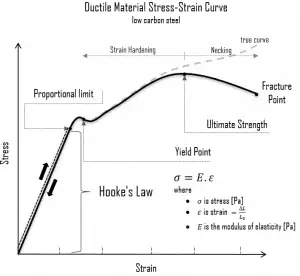 Elastic Deformation. Elastic deformation and elastic strain is a transitory dimensional change that exists only while the initiating stress is applied and disappears immediately upon removing the stress. When a metal is subjected to a load (force), it is distorted or deformed, no matter how strong the metal or light the load. This deformation may or may not be permanent. Up to limiting stress, a body will be able to recover its dimensions on the removal of the load. The applied stresses cause the atoms in a crystal to move from their equilibrium position. All the atoms are displaced the same amount and maintain their relative geometry. When the stresses are removed, all the atoms return to their original positions, and no permanent deformation occurs.
Elastic Deformation. Elastic deformation and elastic strain is a transitory dimensional change that exists only while the initiating stress is applied and disappears immediately upon removing the stress. When a metal is subjected to a load (force), it is distorted or deformed, no matter how strong the metal or light the load. This deformation may or may not be permanent. Up to limiting stress, a body will be able to recover its dimensions on the removal of the load. The applied stresses cause the atoms in a crystal to move from their equilibrium position. All the atoms are displaced the same amount and maintain their relative geometry. When the stresses are removed, all the atoms return to their original positions, and no permanent deformation occurs.- Plastic Deformation. Plastic deformation and plastic strain is a dimensional change that does not disappear when the initiating stress is removed. If the limiting load is exceeded, the body will experience permanent deformation on the removal of the load. Plastic deformation occurs in material bodies after stresses have attained a threshold value known as the elastic limit or yield stress and result from a slip or dislocation mechanism at the atomic level.