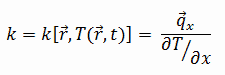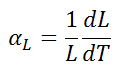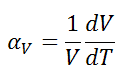Thermal properties of materials refer to the response of materials to changes in their temperature and to the application of heat. As a solid absorbs energy in the form of heat, its temperature rises and its dimensions increase. But different materials react to the application of heat differently.
Heat capacity, thermal expansion, and thermal conductivity are often critical in solids’ practical use.
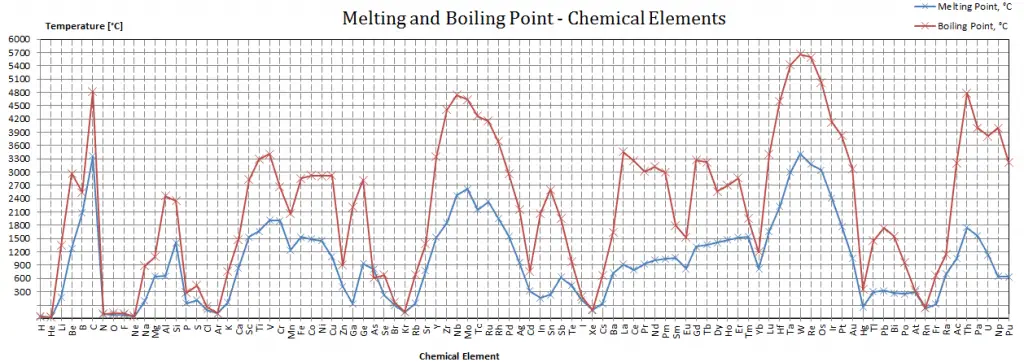
Melting Point – Boiling Point of Materials
Note that these points are associated with the standard atmospheric pressure.
Melting Point
See also: Melting Points – Periodic Table
In general, melting is a phase change of a substance from the solid to the liquid phase. The melting point of a substance is the temperature at which this phase change occurs. The melting point also defines a condition where the solid and liquid can exist in equilibrium, and adding heat will convert the solid into a liquid with no temperature change. At the melting point, the two phases of a substance, liquid and vapor, have identical free energies and therefore are equally likely to exist. Below the melting point, the solid is the more stable state of the two, whereas above the liquid form is preferred. The melting point of a substance depends on pressure and is usually specified at standard pressure. When considered as the temperature of the reverse change from liquid to solid, it is referred to as the freezing or crystallization point.
See also: Melting Point Depression
The first theory explaining the mechanism of melting in bulk was proposed by Lindemann, who used the vibration of atoms in the crystal to explain the melting transition. Solids are similar to liquids in that both are condensed states, with particles far closer together than a gas. The atoms in a solid are tightly bound to each other, either in a regular geometric lattice (crystalline solids, which include metals and ordinary ice) or irregularly (an amorphous solid such as common window glass) and are typically low in energy. The motion of individual atoms, ions, or molecules in a solid is restricted to vibrational motion about a fixed point. As a solid is heated, its particles vibrate more rapidly as the solid absorbs kinetic energy. At some point, the amplitude of vibration becomes so large that the atoms start to invade the space of their nearest neighbors and disturb them, and the melting process initiates. The melting point is the temperature at which the disruptive vibrations of the solid particles overcome the attractive forces operating within the solid.
As with boiling points, a solid’s melting point depends on the strength of those attractive forces. For example, sodium chloride (NaCl) is an ionic compound with many strong ionic bonds, and sodium chloride melts at 801°C. On the other hand, ice (solid H2O) is a molecular compound whose molecules are held together by hydrogen bonds, effectively a strong example of an interaction between two permanent dipoles. Though hydrogen bonds are the strongest of the intermolecular forces, the strength of hydrogen bonds is much less than that of ionic bonds. The melting point of ice is 0 °C.
Covalent bonds often form small collections of better-connected atoms called molecules, which in solids and liquids are bound to other molecules by forces that are often much weaker than the covalent bonds that hold the molecules internally together. Such weak intermolecular bonds give organic molecular substances, such as waxes and oils, their soft bulk character and their low melting points (in liquids, molecules must cease most structured or oriented contact with each other).
Boiling Point
See also: Boiling Points – Periodic Table
In general, boiling is a phase change of a substance from the liquid to the gas phase. The boiling point of a substance is the temperature at which this phase change (boiling or vaporization) occurs. The temperature at which vaporization (boiling) starts to occur for a given pressure is also known as the saturation temperature. At this condition, a mixture of vapor and liquid can exist together. The liquid can be saturated with thermal energy and any addition of thermal energy results in a phase transition. At the boiling point, the two phases of a substance, liquid and vapor, have identical free energies and therefore are equally likely to exist. Below the boiling point, the liquid is the more stable state of the two, whereas the gaseous form is preferred above. The pressure at which vaporization (boiling) starts to occur for a given temperature is called the saturation pressure. When considered as the temperature of the reverse change from vapor to liquid, it is referred to as the condensation point.
As can be seen, the boiling point of a liquid varies depending upon the surrounding environmental pressure. A liquid in a partial vacuum has a lower boiling point than when that liquid is at atmospheric pressure. A liquid at high pressure has a higher boiling point than when that liquid is at atmospheric pressure. For example, water boils at 100°C (212°F) at sea level but 93.4°C (200.1°F) at 1900 meters (6,233 ft) altitude. On the other hand, water boils at 350°C (662°F) at 16.5 MPa (typical pressure of PWRs).
In the periodic table of elements, the element with the lowest boiling point is helium. Both the boiling points of rhenium and tungsten exceed 5000 K at standard pressure. Since it is difficult to measure extreme temperatures without bias, both have been cited in the literature as having the higher boiling point.
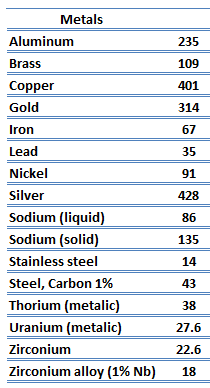
Thermal Conductivity of Materials
The heat transfer characteristics of solid material are measured by a property called the thermal conductivity, k (or λ), measured in W/m.K. It measures a substance’s ability to transfer heat through a material by conduction. Note that Fourier’s law applies to all matter, regardless of its state (solid, liquid, or gas). Therefore, it is also defined for liquids and gases.
The thermal conductivity of most liquids and solids varies with temperature, and for vapors, it also depends upon pressure. In general:
Most materials are nearly homogeneous. Therefore we can usually write k = k (T). Similar definitions are associated with thermal conductivities in the y- and z-directions (ky, kz), but for an isotropic material, the thermal conductivity is independent of the direction of transfer, kx = ky = kz = k.
Thermal Conductivity of Metals
- the migration of free electrons
- lattice vibrational waves (phonons)
When electrons and phonons carry thermal energy leading to conduction heat transfer in a solid, the thermal conductivity may be expressed as:
k = ke + kph
Metals are solids, and as such, they possess a crystalline structure where the ions (nuclei with their surrounding shells of core electrons) occupy translationally equivalent positions in the crystal lattice. Metals, in general, have high electrical conductivity, high thermal conductivity, and high density. Accordingly, the transport of thermal energy may be due to two effects:
- the migration of free electrons
- lattice vibrational waves (phonons).
When electrons and phonons carry thermal energy leading to conduction heat transfer in a solid, the thermal conductivity may be expressed as:
k = ke + kph
The unique feature of metals, as far as their structure is concerned, is the presence of charge carriers, specifically electrons. The electrical and thermal conductivities of metals originate from their outer electrons being delocalized, and their contribution to the thermal conductivity is referred to as the electronic thermal conductivity, ke. In fact, in pure metals such as gold, silver, copper, and aluminum, the heat current associated with the flow of electrons far exceeds a small contribution due to the flow of phonons. In contrast, for alloys, the contribution of kph to k is no longer negligible.
Thermal Conductivity of Nonmetals
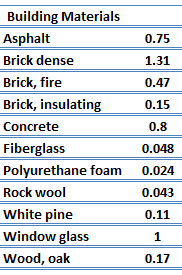For nonmetallic solids, k is determined primarily by kph, which increases as the frequency of interactions between the atoms and the lattice decreases. Lattice thermal conduction is the dominant thermal conduction mechanism in nonmetals, if not the only one. In solids, atoms vibrate about their equilibrium positions (crystal lattice). The vibrations of atoms are not independent of each other but are rather strongly coupled with neighboring atoms. The regularity of the lattice arrangement has an important effect on kph, with crystalline (well-ordered) materials like quartz having a higher thermal conductivity than amorphous materials like glass at sufficiently high temperatures of kph ∝ 1/T.
The quanta of the crystal vibrational field are referred to as “phonons.” A phonon is a collective excitation in a periodic, elastic arrangement of atoms or molecules in condensed matter, like solids and some liquids. Phonons play a major role in many physical properties of condensed matter, like thermal and electrical conductivity. In fact, for crystalline, nonmetallic solids such as diamond, kph can be quite large, exceeding values of k associated with good conductors, such as aluminum. In particular, diamond has the highest hardness and thermal conductivity (k = 1000 W/m.K) of any bulk material.
Thermal Conductivity of Liquids and Gases
In physics, a fluid is a substance that continually deforms (flows) under applied shear stress. Fluids are a subset of the phases of matter and include liquids, gases, plasmas, and, to some extent, plastic solids. Because the intermolecular spacing is much larger and the motion of the molecules is more random for the fluid state than for the solid state, thermal energy transport is less effective. Therefore, the thermal conductivity of gases and liquids is generally smaller than that of solids. In liquids, thermal conduction is caused by atomic or molecular diffusion. In gases, thermal conduction is caused by the diffusion of molecules from a higher energy level to a lower level.
Thermal Conductivity of Gases
The effect of temperature, pressure and chemical species on the thermal conductivity of a gas may be explained in terms of the kinetic theory of gases. Air and other gases are generally good insulators, in the absence of convection. Therefore, many insulating materials (e.g., polystyrene) function simply by having a large number of gas-filled pockets which prevent large-scale convection. Alternation of gas pocket and solid material causes the heat must be transferred through many interfaces causing a rapid decrease in heat transfer coefficient.
The thermal conductivity of gases is directly proportional to the density of the gas, the mean molecular speed, and especially the mean free path of a molecule. The mean free path also depends on the diameter of the molecule, with larger molecules more likely to experience collisions than small molecules, which is the average distance traveled by an energy carrier (a molecule) before experiencing a collision. Light gases, such as hydrogen and helium, typically have high thermal conductivity, and dense gases such as xenon and dichlorodifluoromethane have low thermal conductivity.
In general, the thermal conductivity of gases increases with increasing temperature.
Thermal Conductivity of Liquids
As was written, thermal conduction in liquids is caused by atomic or molecular diffusion, but physical mechanisms for explaining the thermal conductivity of liquids are not well understood. Liquids tend to have better thermal conductivity than gases, and the ability to flow makes a liquid suitable for removing excess heat from mechanical components. The heat can be removed by channeling the liquid through a heat exchanger. The coolants used in nuclear reactors include water or liquid metals, such as sodium or lead.
The thermal conductivity of nonmetallic liquids generally decreases with increasing temperature.
Coefficient of Thermal Expansion of Materials
Thermal expansion is generally the tendency of matter to change its dimensions in response to a change in temperature. It is usually expressed as a fractional change in length or volume per unit temperature change. Thermal expansion is common for solids, liquids, and gases. Unlike gases or liquids, solid materials keep their shape when undergoing thermal expansion. A linear expansion coefficient is usually employed in describing the expansion of a solid, while a volume expansion coefficient is more useful for a liquid or a gas.
The linear thermal expansion coefficient is defined as:
where L is a particular length measurement and dL/dT is the rate of change of that linear dimension per unit change in temperature.
The volumetric thermal expansion coefficient is the most basic thermal expansion coefficient and the most relevant for fluids. Substances generally expand or contract when their temperature changes, with expansion or contraction occurring in all directions.
The volumetric thermal expansion coefficient is defined as:
where L is the volume of the material, and dV/dT is the rate of change of that volume per unit change in temperature.
In a solid or liquid, there is a dynamic balance between the cohesive forces holding the atoms or molecules together and the conditions created by temperature. Therefore higher temperatures imply a greater distance between atoms. Different materials have different bonding forces and, therefore, different expansion coefficients. If a crystalline solid is isometric (with the same structural configuration throughout), the expansion will be uniform in all crystal dimensions. For these materials, the area and volumetric thermal expansion coefficient are approximately twice and three times larger than the linear thermal expansion coefficient (αV = 3αL). If it is not isometric, there may be different expansion coefficients for different crystallographic directions, and the crystal will change shape as the temperature changes.
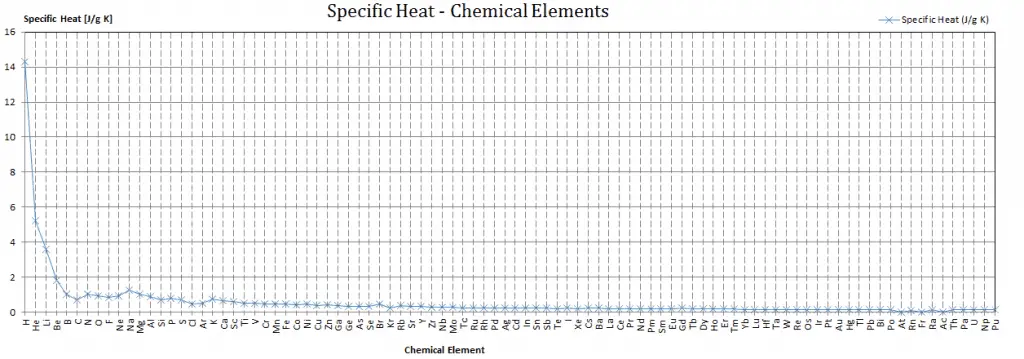
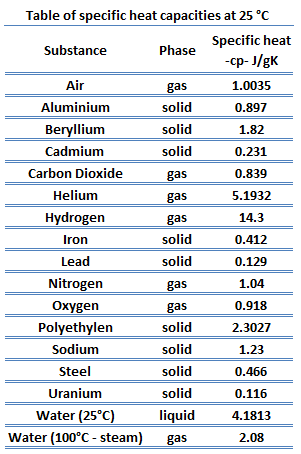
Specific Heat of Materials
Specific heat, or specific heat capacity, is a property related to internal energy that is very important in thermodynamics. The intensive properties cv and cp are defined for pure, simple compressible substances as partial derivatives of the internal energy u(T, v) and enthalpy h(T, p), respectively:
where the subscripts v and p denote the variables held fixed during differentiation. The properties cv and cp are referred to as specific heat (or heat capacities) because, under certain special conditions, they relate the temperature change of a system to the amount of energy added by heat transfer. Their SI units are J/kg K or J/mol K.
Different substances are affected to different magnitudes by the addition of heat. When a given amount of heat is added to different substances, their temperatures increase by different amounts.
Heat capacity is an extensive property of matter, meaning it is proportional to the size of the system. Heat capacity C has the energy unit per degree or kelvin. When expressing the same phenomenon as an intensive property, the heat capacity is divided by the amount of substance, mass, or volume. Thus the quantity is independent of the size or extent of the sample.
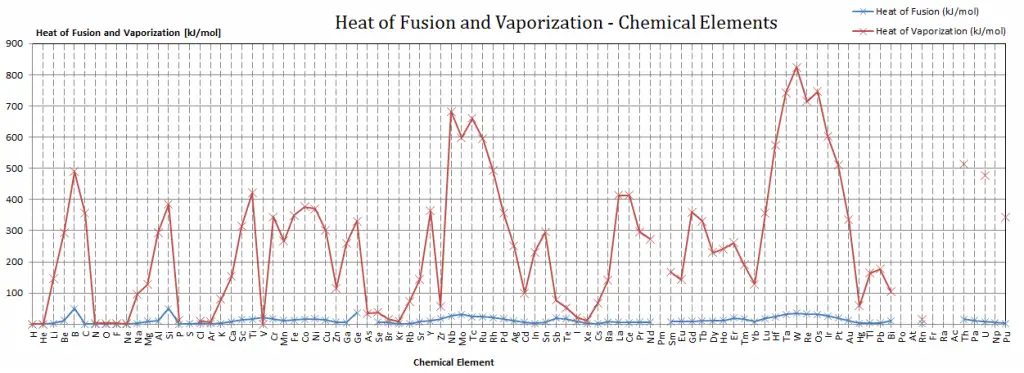
Latent Heat of Vaporization of Materials
Generally, when a material changes phase from solid to liquid or liquid to gas, a certain amount of energy is involved in this change of phase. In the case of liquid to gas phase change, this amount of energy is known as the enthalpy of vaporization (symbol ∆Hvap; unit: J), also known as the (latent) heat of vaporization or heat of evaporation. For example, see the figure, which describes the phase transitions of water.
Latent heat is the amount of heat added to or removed from a substance to produce a phase change. This energy breaks down the intermolecular attractive forces and must provide the energy necessary to expand the gas (the pΔV work). When latent heat is added, no temperature change occurs. The enthalpy of vaporization is a function of the pressure at which that transformation takes place.
The temperature at which vaporization (boiling) starts to occur for a given pressure is also known as the saturation temperature. At this condition, a mixture of vapor and liquid can exist together. The liquid can be saturated with thermal energy and any addition of thermal energy results in a phase transition. At the boiling point, the two phases of a substance, liquid and vapor, have identical free energies and therefore are equally likely to exist. Below the boiling point, the liquid is the more stable state of the two, whereas the gaseous form is preferred above.
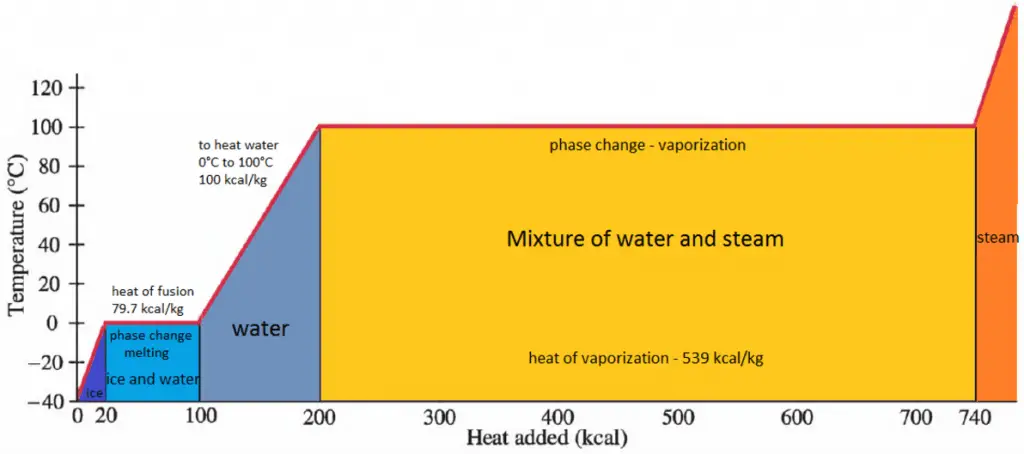
Latent Heat of Fusion of Materials
In the case of solid to liquid phase change, the change in enthalpy required to change its state is known as the enthalpy of fusion (symbol ∆Hfus; unit: J), also known as the (latent) heat of fusion. Latent heat is the amount of heat added to or removed from a substance to produce a phase change. This energy breaks down the intermolecular attractive forces and must provide the energy necessary to expand the system (the pΔV work).
The liquid phase has higher internal energy than the solid phase. This means energy must be supplied to a solid to melt it and energy is released from a liquid when it freezes because the molecules in the liquid experience weaker intermolecular forces and have higher potential energy (a kind of bond-dissociation energy for intermolecular forces).
The temperature at which the phase transition occurs is the melting point. The melting point also defines a condition where the solid and liquid can exist in equilibrium. Adding heat will convert the solid into a liquid with no temperature change. At the melting point the two phases of a substance, liquid, and vapor, have identical free energies and therefore are equally likely to exist. Below the melting point, the solid is the more stable state of the two, whereas above, the liquid form is preferred. The melting point of a substance depends on pressure and is usually specified at standard pressure. When considered as the temperature of the reverse change from liquid to solid, it is referred to as the freezing or crystallization point.
Emissivity of Materials
The emissivity, ε, of the surface of a material is its effectiveness in emitting energy as thermal radiation and varies between 0.0 and 1.0.
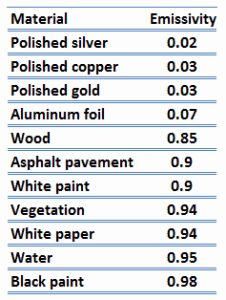A blackbody in thermal equilibrium has an emissivity of ε = 1.0. Real objects do not radiate as much heat as a perfect black body; they radiate less heat than a black body and are called gray bodies. The Stefan-Boltzmann law must include emissivity to consider that real objects are gray bodies. Quantitatively, emissivity is the ratio of the thermal radiation from a surface to the radiation from an ideal black surface at the same temperature as given by the Stefan–Boltzmann law. Emissivity is simply a factor by which we multiply the black body heat transfer to consider that the black body is the ideal case.
The surface of a blackbody emits thermal radiation at the rate of approximately 448 watts per square meter at room temperature (25 °C, 298.15 K). Real objects with emissivities less than 1.0 (e.g., copper wire) emit radiation at correspondingly lower rates (e.g., 448 x 0.03 = 13.4 W/m2). Emissivity plays an important role in heat transfer problems. For example, solar heat collectors incorporate selective surfaces that have very low emissivities. These collectors waste very little of the solar energy through the emission of thermal radiation.
Another important radiation property of a surface is its absorptivity, α, which is the fraction of the radiation energy incident on a surface that is absorbed by the surface. Like emissivity, value of absorptivity is in the range 0 < α < 1.
In general, absorptivity and emissivity are interconnected by Kirchhoff’s Law of thermal radiation, which states:
For an arbitrary body emitting and absorbing thermal radiation in thermodynamic equilibrium, the emissivity is equal to the absorptivity.
emissivity ε = absorptivity α
Note that visible radiation occupies a very narrow band of the spectrum from 400 to 760 nm, we cannot make any judgments about the blackness of a surface on the basis of visual observations. For example, consider a white paper that reflects visible light and thus appears white. On the other hand, it is essentially black for infrared radiation (absorptivity α = 0.94) since they strongly absorb long-wavelength radiation.
See also: Thermal Blanket
