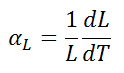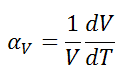Thermal properties of materials refer to the response of materials to changes in their temperature and the application of heat. As a solid absorbs energy in the form of heat, its temperature rises, and its dimensions increase. But different materials react to the application of heat differently.
Heat capacity, thermal expansion, and thermal conductivity are often critical in solids’ practical use.
Coefficient of Thermal Expansion of Materials
Thermal expansion is generally the tendency of matter to change its dimensions in response to a change in temperature. It is usually expressed as a fractional change in length or volume per unit temperature change. Thermal expansion is common for solids, liquids, and gases. Unlike gases or liquids, solid materials keep their shape when undergoing thermal expansion. A linear expansion coefficient is usually employed in describing the expansion of a solid, while a volume expansion coefficient is more useful for a liquid or a gas.
The linear thermal expansion coefficient is defined as:
where L is a particular length measurement and dL/dT is the rate of change of that linear dimension per unit change in temperature.
The volumetric thermal expansion coefficient is the most basic thermal expansion coefficient and the most relevant for fluids. Substances generally expand or contract when their temperature changes, with expansion or contraction occurring in all directions.
The volumetric thermal expansion coefficient is defined as:
where L is the volume of the material, and dV/dT is the rate of change of that volume per unit change in temperature.
In a solid or liquid, there is a dynamic balance between the cohesive forces holding the atoms or molecules together and the conditions created by temperature. Therefore higher temperatures imply a greater distance between atoms. Different materials have different bonding forces and, therefore, different expansion coefficients. If a crystalline solid is isometric (with the same structural configuration throughout), the expansion will be uniform in all crystal dimensions. For these materials, the area and volumetric thermal expansion coefficient are approximately twice and three times larger than the linear thermal expansion coefficient (αV = 3αL). If it is not isometric, there may be different expansion coefficients for different crystallographic directions, and the crystal will change shape as the temperature changes.