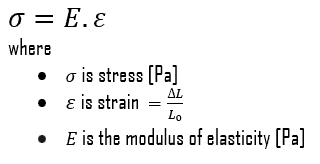Alloys are usually stronger than pure metals, although they generally offer reduced electrical and thermal conductivity. Strength is the most important criterion by which many structural materials are judged. Therefore, alloys are used for engineering construction. Steel, probably the most common structural metal, is a good example of an alloy. It is an alloy of iron and carbon, with other elements to give it certain desirable properties.
It is sometimes possible for a material to be composed of several solid phases. The strengths of these materials are enhanced by allowing a solid structure to become a form composed of two interspersed phases. When the material in question is an alloy, it is possible to quench the metal from a molten state to form the interspersed phases. Quenching refers to a heat treatment in which a material is rapidly cooled in water, oil, or air to obtain certain material properties, especially hardness. In metallurgy, quenching is commonly used to harden steel by introducing martensite.
Strength of Metal Alloys
In the mechanics of materials, the strength of a material is its ability to withstand an applied load without failure or plastic deformation. The strength of materials considers the relationship between the external loads applied to a material and the resulting deformation or change in material dimensions. The strength of a material is its ability to withstand this applied load without failure or plastic deformation.
Ultimate Tensile Strength
The ultimate tensile strength is the maximum on the engineering stress-strain curve. This corresponds to the maximum stress sustained by a structure in tension. Ultimate tensile strength is often shortened to “tensile strength” or “the ultimate.” If this stress is applied and maintained, a fracture will result. Often, this value is significantly more than the yield stress (as much as 50 to 60 percent more than the yield for some types of metals). When a ductile material reaches its ultimate strength, it experiences necking where the cross-sectional area reduces locally. The stress-strain curve contains no higher stress than the ultimate strength. Even though deformations can continue to increase, the stress usually decreases after achieving the ultimate strength. It is an intensive property; therefore, its value does not depend on the size of the test specimen. However, it depends on other factors, such as the preparation of the specimen, the presence or otherwise of surface defects, and the temperature of the test environment and material. Ultimate tensile strengths vary from 50 MPa for an aluminum to as high as 3000 MPa for very high-strength steel.
Example – Ultimate Tensile Strength – Low-carbon Steel
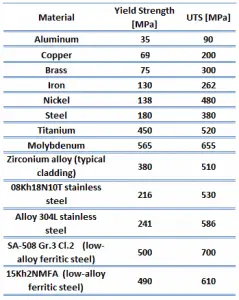
The ultimate tensile strength of low-carbon steel is between 400 – 550 MPa.
Example – Ultimate Tensile Strength – Ultra-high-carbon Steel
The ultimate tensile strength of ultra-high-carbon steel is 1100 MPa.
Yield Strength
The yield point is the point on a stress-strain curve that indicates the limit of elastic behavior and the beginning plastic behavior. Yield strength or yield stress is the material property defined as the stress at which a material begins to deform plastically. In contrast, the yield point is where nonlinear (elastic + plastic) deformation begins. Before the yield point, the material will deform elastically and return to its original shape when the applied stress is removed. Once the yield point is passed, some fraction of the deformation will be permanent and non-reversible. Some steels and other materials exhibit a behavior termed a yield point phenomenon. Yield strengths vary from 35 MPa for low-strength aluminum to greater than 1400 MPa for high-strength steel.
Example – Yield Strength – Low-carbon Steel
The yield strength of low-carbon steel is 250 MPa.
Example – Yield Strength – Ultra-high-carbon Steel
The yield strength of ultra-high-carbon steel is 800 MPa.
Young’s Modulus of Elasticity
Young’s modulus of elasticity is the elastic modulus for tensile and compressive stress in the linear elasticity regime of a uniaxial deformation and is usually assessed by tensile tests. Up to limiting stress, a body will be able to recover its dimensions on the removal of the load. The applied stresses cause the atoms in a crystal to move from their equilibrium position, and all the atoms are displaced the same amount and maintain their relative geometry. When the stresses are removed, all the atoms return to their original positions, and no permanent deformation occurs. According to Hooke’s law, the stress is proportional to the strain (in the elastic region), and the slope is Young’s modulus. Young’s modulus is equal to the longitudinal stress divided by the strain.
Example – Young’s modulus of elasticity – Low-carbon Steel
Young’s modulus of elasticity of low-carbon steel is 200 GPa.
