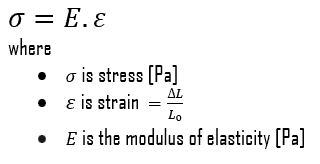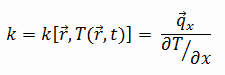Medium-carbon steel has approximately 0.3–0.6% carbon content. These alloys may be heat-treated by austenitizing, quenching, and then tempering to improve their mechanical properties. They are most often utilized in tempered conditions, having microstructures of tempered martensite. Medium-carbon steel balances ductility and strength and has good wear resistance. This grade of steel is mostly used in the production of machine components, shafts, axles, gears, crankshafts, coupling, and forgings. It could also be used in rails, railway wheels, other machine parts, and high-strength structural components calling for a combination of high strength, wear resistance, and toughness.
For example, 1040 steel is plain carbon steel containing 0.40 wt% C. Typical uses of this type of steel include machine, plow, carriage bolts, tie wire, cylinder head studs, machined parts, U-bolts, concrete reinforcing rods, and forgings.
Price of Medium-carbon Steel
It isn’t easy to know the exact cost of the different materials because it strongly depends on many variables such as:
- the type of product you would like to buy
- the amount of the product
- the exact type of material
Raw materials prices change daily and are primarily driven by supply, demand, and energy prices.
However, as a rule of thumb, stainless steel cost four to five times much as carbon steel in material costs. Carbon steel is about $500/ton, while stainless steel costs about $2000/ton. The more alloying elements the steel contains, the more expensive it is. Based on that rule, it is logical to assume that the 316L austenitic stainless steel and the 13% Cr martensitic stainless steel will cost less than the 22% Cr and the 25% Cr duplex stainless steel. The nickel-based steels would probably cost around the price of the duplex stainless steels. Numerous kinds of steel, from low to high carbon, and a wide range of evaluations of stainless steel change immensely in expense. For example, Inconel 600 (registered trademark of Special Metals), which is one of a family of austenitic nickel-chromium-based superalloys, costs about $40000/ton.
Properties of Medium-carbon Steel – AISI 1040 steel
Material properties are intensive properties, which means they are independent of the amount of mass and may vary from place to place within the system at any moment. Materials science involves studying materials’ structure and relating them to their properties (mechanical, electrical, etc.). Once materials scientist knows about this structure-property correlation, they can then go on to study the relative performance of a material in a given application. The major determinants of the structure of a material and thus of its properties are its constituent chemical elements and how it has been processed into its final form.
Mechanical Properties of Medium-carbon Steel – AISI 1040 steel
Materials are frequently chosen for various applications because they have desirable combinations of mechanical characteristics. For structural applications, material properties are crucial, and engineers must consider them.
Strength of Medium-carbon Steel – AISI 1040 steel
In the mechanics of materials, the strength of a material is its ability to withstand an applied load without failure or plastic deformation. The strength of materials considers the relationship between the external loads applied to a material and the resulting deformation or change in material dimensions. The strength of a material is its ability to withstand this applied load without failure or plastic deformation.
Ultimate Tensile Strength
The ultimate tensile strength of medium-carbon steel is 620 MPa.
 The ultimate tensile strength is the maximum on the engineering stress-strain curve. This corresponds to the maximum stress sustained by a structure in tension. Ultimate tensile strength is often shortened to “tensile strength” or “the ultimate.” If this stress is applied and maintained, a fracture will result. Often, this value is significantly more than the yield stress (as much as 50 to 60 percent more than the yield for some types of metals). When a ductile material reaches its ultimate strength, it experiences necking where the cross-sectional area reduces locally. The stress-strain curve contains no higher stress than the ultimate strength. Even though deformations can continue to increase, the stress usually decreases after achieving the ultimate strength. It is an intensive property; therefore, its value does not depend on the size of the test specimen. However, it depends on other factors, such as the preparation of the specimen, the presence or otherwise of surface defects, and the temperature of the test environment and material. Ultimate tensile strengths vary from 50 MPa for aluminum to as high as 3000 MPa for very high-strength steel.
The ultimate tensile strength is the maximum on the engineering stress-strain curve. This corresponds to the maximum stress sustained by a structure in tension. Ultimate tensile strength is often shortened to “tensile strength” or “the ultimate.” If this stress is applied and maintained, a fracture will result. Often, this value is significantly more than the yield stress (as much as 50 to 60 percent more than the yield for some types of metals). When a ductile material reaches its ultimate strength, it experiences necking where the cross-sectional area reduces locally. The stress-strain curve contains no higher stress than the ultimate strength. Even though deformations can continue to increase, the stress usually decreases after achieving the ultimate strength. It is an intensive property; therefore, its value does not depend on the size of the test specimen. However, it depends on other factors, such as the preparation of the specimen, the presence or otherwise of surface defects, and the temperature of the test environment and material. Ultimate tensile strengths vary from 50 MPa for aluminum to as high as 3000 MPa for very high-strength steel.
Yield Strength
The yield strength of medium-carbon steel is 420 MPa.
The yield point is the point on a stress-strain curve that indicates the limit of elastic behavior and the beginning plastic behavior. Yield strength or yield stress is the material property defined as the stress at which a material begins to deform plastically. In contrast, the yield point is the point where nonlinear (elastic + plastic) deformation begins. Before the yield point, the material will deform elastically and return to its original shape when the applied stress is removed. Once the yield point is passed, some fraction of the deformation will be permanent and non-reversible. Some steels and other materials exhibit a behavior termed a yield point phenomenon. Yield strengths vary from 35 MPa for low-strength aluminum to greater than 1400 MPa for high-strength steel.
Young’s Modulus of Elasticity
Young’s modulus of elasticity of medium-carbon steel is 200 GPa.
Young’s modulus of elasticity is the elastic modulus for tensile and compressive stress in the linear elasticity regime of a uniaxial deformation and is usually assessed by tensile tests. Up to limiting stress, a body will be able to recover its dimensions on the removal of the load. The applied stresses cause the atoms in a crystal to move from their equilibrium position, and all the atoms are displaced the same amount and maintain their relative geometry. When the stresses are removed, all the atoms return to their original positions and no permanent deformation occurs. According to Hooke’s law, the stress is proportional to the strain (in the elastic region), and the slope is Young’s modulus. Young’s modulus is equal to the longitudinal stress divided by the strain.
The hardness of Medium-carbon Steel – AISI 1040 steel
Brinell hardness of medium-carbon steel is approximately 200 MPa.
 In materials science, hardness is the ability to withstand surface indentation (localized plastic deformation) and scratching. Hardness is probably the most poorly defined material property because it may indicate resistance to scratching, abrasion, indentation, or even resistance to shaping or localized plastic deformation. Hardness is important from an engineering standpoint because resistance to wear by either friction or erosion by steam, oil, and water generally increases with hardness.
In materials science, hardness is the ability to withstand surface indentation (localized plastic deformation) and scratching. Hardness is probably the most poorly defined material property because it may indicate resistance to scratching, abrasion, indentation, or even resistance to shaping or localized plastic deformation. Hardness is important from an engineering standpoint because resistance to wear by either friction or erosion by steam, oil, and water generally increases with hardness.
Brinell hardness test is one of the indentation hardness tests developed for hardness testing. In Brinell tests, a hard, spherical indenter is forced under a specific load into the surface of the metal to be tested. The typical test uses a 10 mm (0.39 in) diameter hardened steel ball as an indenter with a 3,000 kgf (29.42 kN; 6,614 lbf) force. The load is maintained constant for a specified time (between 10 and 30 s). For softer materials, a smaller force is used; for harder materials, a tungsten carbide ball is substituted for the steel ball.
The test provides numerical results to quantify the hardness of a material, which is expressed by the Brinell hardness number – HB. The Brinell hardness number is designated by the most commonly used test standards (ASTM E10-14[2] and ISO 6506–1:2005) as HBW (H from hardness, B from Brinell, and W from the material of the indenter, tungsten (wolfram) carbide). In former standards, HB or HBS were used to refer to measurements made with steel indenters.
The Brinell hardness number (HB) is the load divided by the surface area of the indentation. The diameter of the impression is measured with a microscope with a superimposed scale. The Brinell hardness number is computed from the equation:
There are various test methods in common use (e.g., Brinell, Knoop, Vickers, and Rockwell). Some tables correlate the hardness numbers from the different test methods where correlation is applicable. In all scales, a high hardness number represents a hard metal.
Thermal Properties of Medium-carbon Steel – AISI 1040 steel
Thermal properties of materials refer to the response of materials to changes in their temperature and the application of heat. As a solid absorbs energy in the form of heat, its temperature rises, and its dimensions increase. But different materials react to the application of heat differently.
Heat capacity, thermal expansion, and thermal conductivity are often critical in solids’ practical use.
Melting Point of Medium-carbon Steel – AISI 1040 steel
The melting point of medium-carbon steel is around 1520°C.
In general, melting is a phase change of a substance from the solid to the liquid phase. The melting point of a substance is the temperature at which this phase change occurs. The melting point also defines a condition where the solid and liquid can exist in equilibrium.
Thermal Conductivity of Medium-carbon Steel – AISI 1040 steel
The thermal conductivity of medium-carbon steel is 50 W/(m. K).
The heat transfer characteristics of solid material are measured by a property called the thermal conductivity, k (or λ), measured in W/m.K. It measures a substance’s ability to transfer heat through a material by conduction. Note that Fourier’s law applies to all matter, regardless of its state (solid, liquid, or gas). Therefore, it is also defined for liquids and gases.
The thermal conductivity of most liquids and solids varies with temperature, and for vapors, it also depends upon pressure. In general:
Most materials are nearly homogeneous. Therefore we can usually write k = k (T). Similar definitions are associated with thermal conductivities in the y- and z-directions (ky, kz). However, for an isotropic material, the thermal conductivity is independent of the transfer direction, kx = ky = kz = k.