For radiation detection systems that record pulses (discrete events), the dead time is the time after each event during which the system cannot record another event. This phenomenon is very important, for example, for Geiger counters. Because of the large avalanche induced by any ionization, a Geiger counter takes a long time (about 1 ms) to recover between successive pulses. Therefore, Geiger counters cannot measure high radiation rates due to the “dead time” of the tube.
In other words, dead-time is when the detector is busy and cannot accept and process pulses. In the case of detectors of ionizing radiation, this phenomenon can have serious consequences since dead-time distorts outputs at high activities or high dose rates. The total dead time of a detection system is usually due to the contributions of the intrinsic dead time of the detector, the analog front end, and the data acquisition.
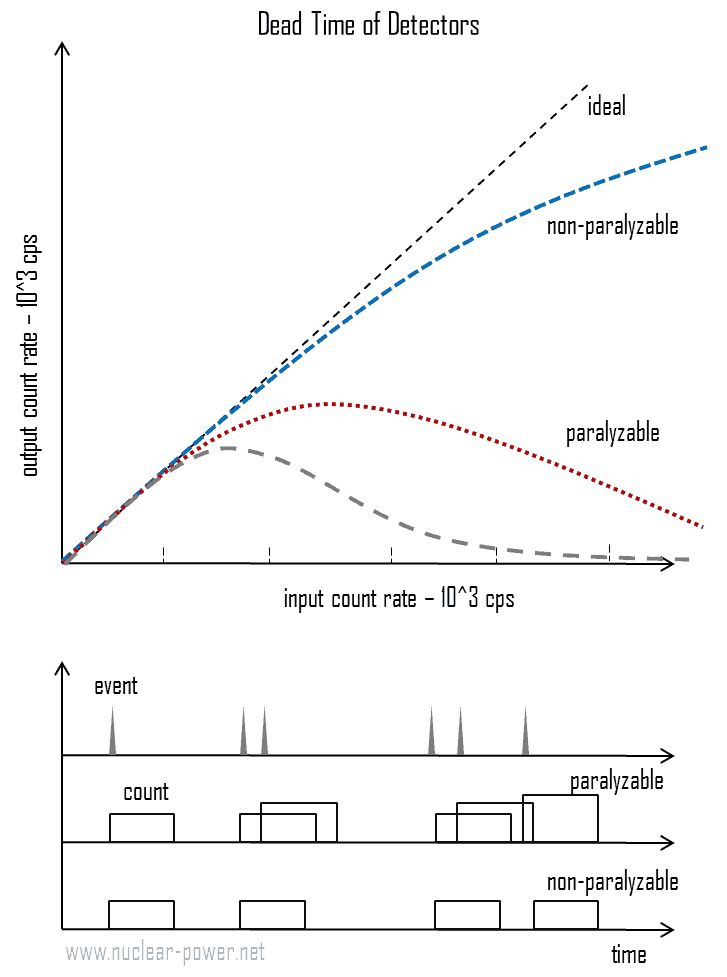
Paralyzable and Non-paralyzable Detector
Because of the random nature of radioactive decay, there is always some probability that a true event will be lost because another event is just recorded, and the detector cannot accept and process more than one pulse.
There are two main dead-time characteristics of each detecting system:
- Paralyzable. In a paralyzable detector, an event happening during the dead time will not just be missed. Still, it will restart the dead time so that with the increasing rate, the detector will reach a saturation point where it will be incapable of recording any event at all.
- Non-paralyzable. In a non-paralyzable detector, an event happening during the dead time is simply lost. With an increasing event rate, the detector will reach a saturation rate equal to the inverse of the dead time.
Quenching – Dead Time – Geiger Counters
The dead time phenomenon is also very important for Geiger counters. Typically it has a value of about 100 μs (for proportional counters, it is much less), so after each ionizing event, a Geiger tube is switched off for 100 μs.
In a Geiger counter, the fill gas of the chamber is an inert gas that is ionized by incident radiation and a quench gas of 5–10% of an organic vapor or a halogen gas to prevent spurious pulsing by quenching the electron avalanches. The Geiger counter should not give spurious pulses and should recover quickly to the passive state, ready for the next radiation event. Argon and helium are the most frequently used fill gases and allow the detection of alpha, beta, and gamma radiation. He-3 and BF3 (Boron Trifluoride) are the most commonly employed for neutron detection.
However, there is a positively charged gas ion left over for each electron collected in the chamber. These gas ions are heavy compared to an electron and move much more slowly. Free electrons are much lighter than positive ions. Thus, they are drawn toward the positive central electrode much faster than the positive ions drawn to the chamber wall. The resulting cloud of positive ions near the electrode leads to distortions in gas multiplication. Eventually, the positive ions move from the positively charged central wire to the negatively charged wall and are neutralized by gaining an electron. These atoms then return to their ground state by emitting photons, which produce further ionization and spurious secondary discharges. The electrons produced by this ionization move toward the central wire and are multiplied en route. This charge pulse is unrelated to the radiation to be detected and can set off a series of pulses. In practice, the termination of the avalanche is improved by the use of “quenching” techniques.
The quenching gas molecules have a weaker affinity for electrons than the chamber gas does; therefore, the ionized atoms of the chamber gas readily take electrons from the quenching gas molecules. Thus, the ionized molecules of quenching gas reach the chamber wall instead of the chamber gas. The ionized molecules of the quenching gas are neutralized by gaining an electron, and the energy liberated does not cause further ionization but causes dissociation of the molecule. This type of quenching is known as self-quenching or internal quenching since tubes stop the discharge without external assistance.
For Geiger counters, external quenching, sometimes called “active quenching” or “electronic quenching,” is also possible. Electronic quenching uses simplistic high-speed control electronics to rapidly remove and re-apply the high voltage between the electrodes for a fixed time after each discharge peak to increase the tube’s maximum count rate and lifetime.
