Detection of beta radiation is very specific because beta particles are more penetrating than alpha particles. On the other hand, a thin aluminum plate can stop them.
To describe the principles of detection of beta radiation, we must understand the interaction of radiation with matter. Each type of particle interacts differently, and therefore, we must describe the interaction of beta particles (radiation as a flow of these particles) separately.
Interaction of Beta Particles with Matter
Beta radiation consists of free electrons or positrons at relativistic speeds. Beta particles (electrons) are much smaller than alpha particles and carry a single negative charge. They are more penetrating than alpha particles, but a thin aluminium plate can stop them. They can travel several meters in the air but deposit less energy at any point along their paths than alpha particles. Similarly, as for heavy charged particles, beta particles transfer energy by:
- Excitation. The charged particle can transfer energy to the atom, raising electrons to higher energy levels.
- Ionization. Ionization can occur when the charged particle has enough energy to remove an electron, creating ion pairs in surrounding matter.
In addition to these interactions, beta particles lose energy through a radiative process known as the bremsstrahlung. From classical theory, when a charged particle is accelerated or decelerated, it must radiate energy, and the deceleration radiation is known as the bremsstrahlung (“braking radiation”).
Summary of types of interactions:
- Inelastic collisions with atomic electrons (Excitation and Ionization)
- Elastic scattering off nuclei
- Bremsstrahlung
- Cherenkov radiation.
- Annihilation (only positrons)
The nature of the interaction of beta radiation with matter is different from alpha radiation, even though beta particles are also charged particles. Beta particles have a much lower mass and reach mostly relativistic energies than alpha particles. Their mass is equal to the mass of the orbital electrons with which they are interacting. Unlike the alpha particle, a much larger fraction of its kinetic energy can be lost in a single interaction. Since the beta particles mostly reach relativistic energies, the nonrelativistic Bethe formula cannot be used. For high-energy electrons, a similar expression has also been derived by Bethe to describe the specific energy loss due to excitation and ionization (the “collisional losses”).
Moreover, beta particles can interact via electron-nuclear interaction (elastic scattering off nuclei), which can significantly change the direction of a beta particle. Therefore their path is not so straightforward. The beta particles follow a very zig-zag path through absorbing material, and this resulting path of the particle is longer than the linear penetration (range) into the material.
Detectors of Beta Radiation
Detectors may also be categorized according to sensitive materials and methods that can be utilized to make a measurement:
Detection of Beta Radiation using Ionization Chamber
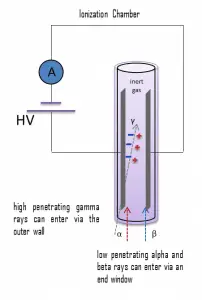For alpha and beta particles to be detected by ionization chambers, they must be given a thin window. This “end-window” must be thin enough for the alpha and beta particles to penetrate. However, a window of almost any thickness will prevent an alpha particle from entering the chamber. The window is usually made of mica with a density of about 1.5 – 2.0 mg/cm2.
For example, an ionization chamber may be used to measure tritium in the air. These devices are known as tritium-in-air monitors. Tritium is a radioactive isotope but emits a very weak form of radiation, a low-energy beta particle similar to an electron. It is a pure beta emitter (i.e., beta emitter without accompanying gamma radiation). The electron’s kinetic energy varies, with an average of 5.7 keV, while the remaining energy is carried off by the nearly undetectable electron antineutrino. Such a very low energy of electron causes that the electron cannot penetrate the skin or even does not travel very far in the air. Beta particles from tritium can penetrate only about 6.0 mm of air. Designing a detector whose walls these beta particles can penetrate is practically impossible. Instead, the tritium-in-air monitor pumps the tritium-contaminated air right through an ionization chamber so that all of the energy of the beta particles can be usefully converted to producing ion pairs inside the chamber.
Detection of Beta Radiation using Scintillation Counter
Scintillation counters are used to measure radiation in various applications, including hand-held radiation survey meters, personnel and environmental monitoring for radioactive contamination, medical imaging, radiometric assay, nuclear security, and nuclear plant safety. They are widely used because they can be made inexpensively yet with good efficiency and can measure both the intensity and the energy of incident radiation.
Scintillation counters can be used to detect alpha, beta, and gamma radiation, and they can also be used for the detection of neutrons. For these purposes, different scintillators are used.
- Beta Particles. For the detection of beta particles, organic scintillators can be used. Pure organic crystals include crystals of anthracene, stilbene, and naphthalene. The decay time of this type of phosphor is approximately 10 nanoseconds. This type of crystal is frequently used in the detection of beta particles. Organic scintillators, having a lower Z than inorganic crystals, are best suited for detecting low-energy (< 10 MeV) beta particles.
Detection of Beta Radiation using Semiconductors – Silicon Strip Detectors
Silicon-based detectors are very good for tracking charged particles. A silicon strip detector is an arrangement of strip-like shaped implants acting as charge-collecting electrodes.
Silicon strip detectors 5 x 5 cm2 in the area are quite common and are used in series (just like planes of MWPCs) to determine charged-particle trajectories to position accuracies of the order of several μm in the transverse direction. These implants form a one-dimensional array of diodes on a low-doped, fully depleted silicon wafer. A position-sensitive detector is built by connecting each metalized strip to a charge-sensitive amplifier. Two-dimensional position measurements can be achieved by applying an additional strip like doping on the wafer backside by using double-sided technology. Such devices can measure small impact parameters and thereby determine whether some charged particle originated from a primary collision or was the decay product of a primary particle that traveled a small distance from the original interaction and then decayed.
