Gamma Spectroscopy
In general, gamma spectroscopy studies the energy spectra of gamma-ray sources, such as in the nuclear industry, geochemical investigation, and astrophysics. Spectroscopes, or spectrometers, are sophisticated devices designed to measure the spectral power distribution of a source. The incident radiation generates a signal that allows determining the energy of the incident particle.
Most radioactive sources produce gamma rays of various energies and intensities. Gamma rays frequently accompany the emission of alpha and beta radiation. A gamma-ray energy spectrum can be produced when these emissions are detected and analyzed with a spectroscopy system. Gamma rays from radioactive decay are in the energy range from a few keV to ~8 MeV, corresponding to the typical energy levels in nuclei with reasonably long lifetimes. As was written, they are produced by nuclei decay as they transition from a high energy state to a lower state. A detailed spectrum analysis is typically used to determine the identity and quantity of gamma emitters present in a sample. It is a vital tool in the radiometric assay. The gamma spectrum is characteristic of the gamma-emitting nuclides contained in the source.
Gamma Ray Spectrometer – Gamma-Ray Spectroscope
As was written, the study and analysis of gamma-ray spectra for scientific and technical use are called gamma spectroscopy. Gamma-ray spectrometers are the instruments that observe and collect such data. A gamma-ray spectrometer (GRS) is a sophisticated device for measuring the energy distribution of gamma radiation. For the measurement of gamma rays above several hundred keV, there are two detector categories of major importance, inorganic scintillators such as NaI(Tl) and semiconductor detectors. In the previous articles, we described gamma spectroscopy using a scintillation detector consisting of a suitable scintillator crystal, a photomultiplier tube, and a circuit for measuring the height of the pulses produced by the photomultiplier. The advantages of a scintillation counter are its efficiency (large size and high density) and the possible high precision and counting rates. Due to the high atomic number of iodine, a large number of interactions will result in the complete absorption of gamma-ray energy so that the photo fraction will be high.

But if a perfect energy resolution is required, we must use a germanium-based detector, such as the HPGe detector. Germanium-based semiconductor detectors are most commonly used where a very good energy resolution is required, especially for gamma spectroscopy as well as x-ray spectroscopy. In gamma spectroscopy, germanium is preferred due to its atomic number being much higher than silicon, increasing the probability of gamma-ray interaction. Moreover, germanium has lower average energy necessary to create an electron-hole pair, which is 3.6 eV for silicon and 2.9 eV for germanium. This also provides the latter with a better resolution in energy. The FWHM (full width at half maximum) for germanium detectors is an energy function. For a 1.3 MeV photon, the FWHM is 2.1 keV, which is very low.
Gamma Spectrum Structure – The Cobalt-60 Spectrum
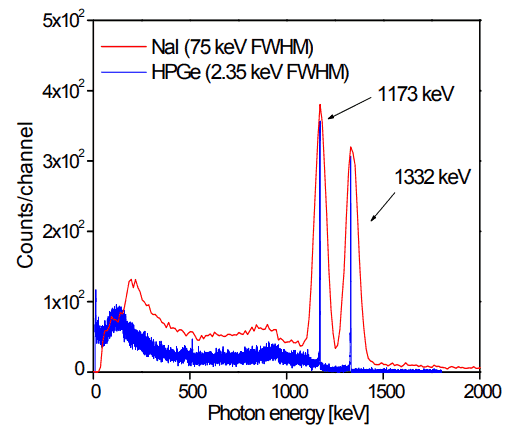
Analysis of gamma spectra is very interesting since it has a structure, and workers must distinguish between true pulses to be analyzed and accompanying pulses from different radiation sources. We will show the structure of the gamma spectrum in the example of cobalt-60 measured by the NaI(Tl) scintillation detector and the HPGe detector. The HPGe detector separates many closely spaced gamma lines, which is very beneficial for measuring multi-gamma emitting radioactive sources.
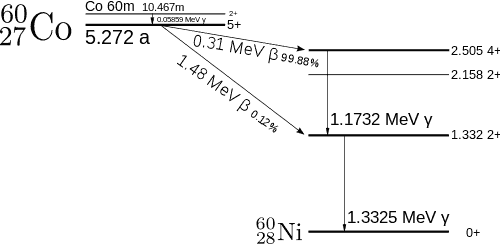
Cobalt-60 is an artificial radioactive isotope of cobalt with a half-life of 5.2747 years. It is synthetically produced by neutron activation of cobalt-59 in nuclear reactors. Cobalt-60 is a common calibration source found in many laboratories. The gamma spectrum has two significant peaks, one at 1173.2 keV and another at 1332.5 keV. Good scintillation detectors should have adequate resolution to separate the two peaks. For HPGe detectors, these peaks are perfectly separated.
As can be seen from the figure, there are two gamma-ray photopeaks. Both detectors also show response at the lower energies, caused by Compton scattering, two smaller escape peaks at energies 0.511 and 1.022 MeV below the photopeak to create electron-positron pairs when one or both annihilation photons escape, and a backscatter peak. Higher energies can be measured when two or more photons strike the detector almost simultaneously, appearing as sum peaks with energies up to the value of two or more photopeaks added.
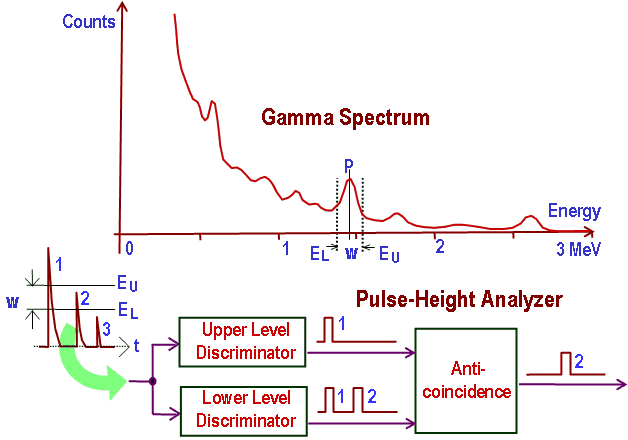
The general structure of the gamma rays spectrum usually has the following principal features:
- Photopeaks are full energy peaks created when γ-ray transfers its full energy (hω −Ebinding) into the sensitive material (scintillation crystal or germanium crystal). Then, a single delta function should be observed in the spectrum. The cobalt-60 spectrum contains two photopeaks, one at 1173.2 keV and another at 1332.5 keV.
- Compton Continuum. In the crystal, a gamma-ray undergoes many interactions, but for intermediate energies, Compton scattering dominates. In Compton scattering, the incident gamma-ray photon is deflected through an angle Θ for its original direction. The photon transfers a portion of its energy to the recoil electron. The energy transferred to the recoil electron can vary from zero to a large fraction (maximum E) of the incident gamma-ray energy because all scattering angles are possible. The size of the scintillation crystal changes the ratio between the photopeak and Compton continuum. For an infinitely large spherical detector centered around a source, no photons would be able to escape, and only a photopeak would be seen on the spectrum. For very small detectors, the chance for a photon to leave after Compton scattering is high, and the Compton continuum would be larger than the photopeak.
- Compton Edge. The Compton edge is a feature of the spectrograph that results from the Compton scattering in the scintillator or detector. This feature is due to photons that undergo Compton scattering with a scattering angle of 180° and then escape the detector. When a gamma-ray scatters off the detector and escapes, only a fraction of its initial energy can be deposited in the sensitive layer of the detector. It depends on the scattering angle of the photon and how much energy will be deposited in the detector. This leads to a spectrum of energies. The Compton edge energy corresponds to a full backscattered photon. The counts between the Compton edge and the photopeaks are caused by multiple Compton scattering events, where scattered gamma photon exits the sensitive material.
Sometimes the structure of the gamma rays spectrum has the following secondary features:
-
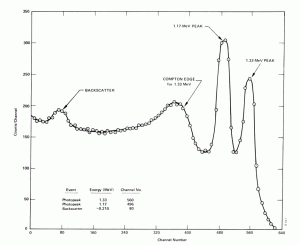
Compton edge of 60Co on gamma spectrometer Na(Tl). Backscatter Peak. A Compton backscatter peak is found when γ-rays enter the material around the detector and are scattered back into the detector. Gamma photon can interact by Compton mechanism in a shield or surrounding materials and is backscattered out of material into sensitive volume. Maximum photon energy in this interaction is ~200 keV regardless of initial photon energy, resulting in a secondary peak at -200 keV.
- X-ray Peaks. When the gamma rays undergo a photoelectric effect in surrounding materials (for example, lead shield), the outgoing X-ray can be captured again by the detector. This gives a characteristic X-ray peak with energy depending on the material it came from. In the case of lead, the characteristic X-ray energies are in the 72-84 keV range. Photoelectric absorption by K-shell electron in the shielding lead results in a K-shell vacancy. The K -> L transition for lead = 72 keV. If this characteristic x-ray is absorbed in the crystal, a secondary peak at 72 keV is observed.
- Coincidence Peak. Simultaneous absorption of two gamma photons in crystal, resulting in a peak higher in energy than the photopeak. The gamma photons may result from serial isomeric transitions (e.g., 2 keV plus 1332.5 keV in case of cobalt-60) or simultaneous decays in separate radionuclides (e.g., 2 x 1173.2 keV in case of cobalt-60).
- Annihilation Peak. For high-energy gamma rays (greater than 1.02 MeV), electron-positron pair production is a possible interaction. But a positron may then annihilate in the detector or the surrounding material. If both 0.51 MeV annihilation photons are absorbed in the crystal, a secondary peak of 1.02 MeV below the photopeak can be found. If one annihilation photon is absorbed and the second exit the crystal, 0.51 MeV is removed from the photopeak, resulting in a secondary peak of 0.51 MeV below the photopeak. The probability is greater that one annihilation photon will be absorbed.