The relationship between a detector’s applied voltage and pulse height is very complex, and pulse height and the number of ion pairs collected are directly related. The Townsend avalanche or Townsend discharge significantly influences the number of ion pairs collected in gaseous ionization detectors. The Townsend avalanche is a gas ionization process where free electrons are accelerated by an electric field, collide with gas molecules, and consequently free secondary electrons. The result is an avalanche multiplication that permits electrical conduction through the gas.
Townsend Avalanche – Proportional Region
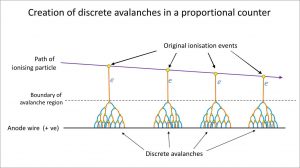
In the proportional region, the charge collected increases with a further increase in the detector voltage, while the number of primary ion pairs remains unchanged. Increasing the voltage provides the primary electrons with sufficient acceleration and energy to ionize additional atoms of the medium. These secondary ions formed are also accelerated, causing an effect known as Townsend avalanches, which creates a single large electrical pulse. Even though there is a large number of secondary ions (about 103 – 105) for each primary event, the chamber is always operated such that the number of secondary ions is proportional to the number of primary events. It is very important because the primary ionization is dependent on the type and energy of the particles or rays in the intercepted radiation field. The number of ion pairs collected divided by the number of ion pairs produced by the primary ionization provides the gas amplification factor (denoted by A). The gas amplification in this region can increase the total amount of ionization to a measurable value. The charge amplification process greatly improves the detector’s signal-to-noise ratio and reduces the subsequent electronic amplification required. The voltage must be kept constant when instruments are operated in the proportional region. If a voltage remains constant, the gas amplification factor also does not change. Proportional counter detection instruments are very sensitive to low levels of radiation. Moreover, proportional counters are capable of particle identification and energy measurement (spectroscopy). Different radiation energies and different radiation types can be distinguished by analyzing the pulse height since they significantly differ in the primary ionization.
Townsend Avalanche – Geiger-Mueller Region
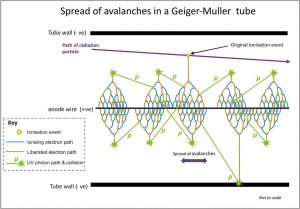
In this region, the voltage is high enough to provide the primary electrons with sufficient acceleration and energy to ionize additional atoms of the medium. These secondary ions (gas amplification) formed are also accelerated, causing an effect known as Townsend avalanches. These avalanches can be triggered and propagated by photons emitted by atoms excited in the original avalanche. Since these photons are not affected by the electric field, they may interact far (e.g., laterally to the axis) from the primary avalanche, and the entire Geiger tube participates in the process. A strong signal (the amplification factor can reach about 1010) is produced by these avalanches with shape and height independently of the primary ionization and the energy of the detected photon. The voltage pulse, in this case, would be a large and easily detectable ≈ 1.6 V.