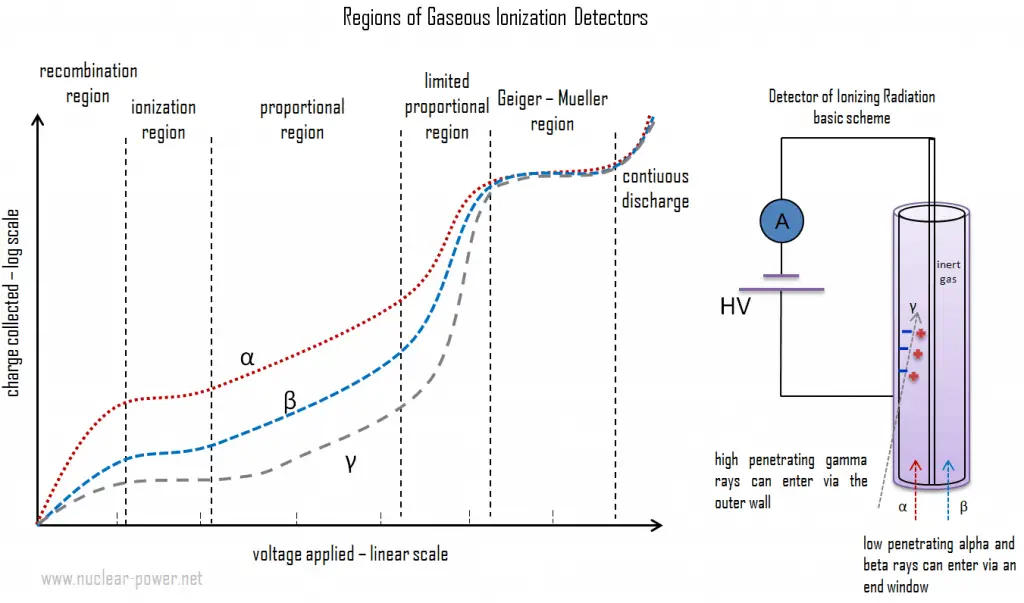
As ionizing radiation enters the gas between the electrodes, a finite number of ion pairs are formed. The average energy needed to produce an ion in the air is about 34 eV. Therefore a 1 MeV radiation completely absorbed in the detector produces about 3 x 104 pairs of ions. The behavior of the resultant ion pairs is affected by the potential gradient of the electric field within the gas and the type and pressure of the fill gas. Under the influence of the electric field, the positive ions will move toward the negatively charged electrode (outer cylinder), and the negative ions (electrons) will migrate toward the positive electrode (central wire). The electric field in this region keeps the ions from recombining with the electrons. Near the anode wire, the field strength becomes large enough to produce Townsend avalanches. This avalanche region occurs only fractions of a millimeter from the anode wire, which is of a very small diameter. This purpose is to use the multiplication effect of the avalanche produced by each ion pair. This is the “avalanche” region. A key design goal is that each original ionizing event due to incident radiation produces only one avalanche. Gas amplification factors can range from unity in the ionization region to 103 or 104 in the proportional region and 1010 in the Geiger-Mueller region. The high amplification factor of the proportional and G-M counters is the major advantage over the ionization chamber. The process of charge amplification greatly improves the signal-to-noise ratio of the detector and reduces the subsequent electronic amplification required.
Gas Amplification in Proportional Region
In the proportional region, the voltage of the detectors is high enough to provide the primary electrons with sufficient acceleration and energy so that they can ionize additional atoms of the medium. These secondary ions (gas amplification) formed are also accelerated, causing an effect known as Townsend avalanches, which creates a single large electrical pulse. Gaseous proportional counters usually operate in high electric fields of 10 kV/cm and achieve typical amplification factors of about 105. Since the amplification factor strongly depends on the applied voltage, the charge collected (output signal) also depends on the applied voltage, and proportional counters require constant voltage.
This is a subtle but important difference between ionization chambers and proportional counters. An ionization chamber will produce a current proportional to the number of electrons collected each second. This current is averaged and is used to drive a display reading in Bq, or μSv/h. Proportional counters do not work in this way. Instead, they amplify each of the individual bursts of ionization so that each ionizing event is detected separately. They, therefore, measure the number of ionizing events (which is why they are called counters).
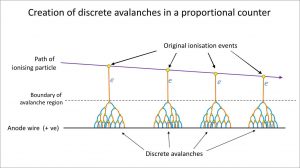
The process of charge amplification greatly improves the signal-to-noise ratio of the detector and reduces the subsequent electronic amplification required. The voltage must be kept constant when instruments are operated in the proportional region, and if a voltage remains constant, the gas amplification factor also does not change. Proportional counter detection instruments are very sensitive to low levels of radiation. The proportional counter can detect alpha, beta, gamma, or neutron radiation in mixed radiation fields by proper functional arrangements, modifications, modifications, and biases. Moreover, proportional counters are capable of particle identification and energy measurement (spectroscopy). The pulse height reflects the energy deposited by the incident radiation in the detector gas. It is possible to distinguish the larger pulses produced by alpha particles from the smaller pulses produced by beta particles or gamma rays.
Gas Amplification in Geiger-Mueller Region
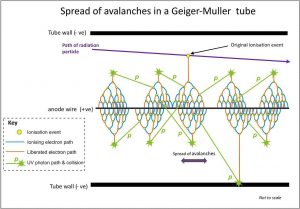
In this region, the voltage is high enough to provide the primary electrons with sufficient acceleration and energy to ionize additional atoms of the medium. These secondary ions (gas amplification) formed are also accelerated, causing an effect known as Townsend avalanches. These avalanches can be triggered and propagated by photons emitted by atoms excited in the original avalanche. Since these photons are not affected by the electric field, they may interact far (e.g., laterally to the axis) from the primary avalanche, and the entire Geiger tube participates in the process. A strong signal (the amplification factor can reach about 1010) is produced by these avalanches with shape and height independently of the primary ionization and the energy of the detected photon. The voltage pulse, in this case, would be a large and easily detectable ≈ 1.6 V.