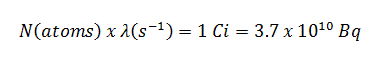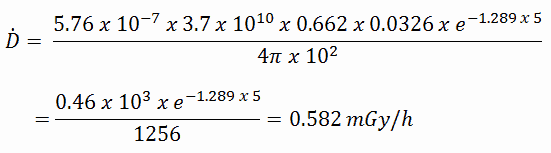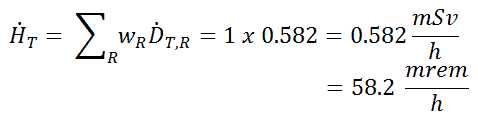 In radiation protection, the rem (an abbreviation for Roentgen Equivalent Man) is the non-SI unit of the equivalent dose used predominantly in the USA. The rem represents the equivalent biological effect of depositing one hundred ergs (one rad) of gamma rays energy in a kilogram of human tissue. The rem is not derived from the unit of exposure, the roentgen. The acronym is now a misleading historical artifact since 1 roentgen deposits about 0.96 rem in soft biological tissue when all weighting factors equal unity.
In radiation protection, the rem (an abbreviation for Roentgen Equivalent Man) is the non-SI unit of the equivalent dose used predominantly in the USA. The rem represents the equivalent biological effect of depositing one hundred ergs (one rad) of gamma rays energy in a kilogram of human tissue. The rem is not derived from the unit of exposure, the roentgen. The acronym is now a misleading historical artifact since 1 roentgen deposits about 0.96 rem in soft biological tissue when all weighting factors equal unity.
As was written, the rem is used for radiation quantities such as equivalent and effective doses. Equivalent dose (symbol HT) is a dose quantity calculated for individual organs (index T – tissue). The equivalent dose is based on the absorbed dose to an organ, adjusted to account for the effectiveness of the type of radiation. The SI unit of HT is the sievert (Sv) or but rem (roentgen equivalent man) is still commonly used (1 Sv = 100 rem).
REM and RAD
For radiation protection purposes, the absorbed dose is averaged over an organ or tissue, T. This absorbed dose average is weighted for the radiation quality in terms of the radiation weighting factor, wR, for the type and energy of radiation incident on the body. The radiation weighting factor is a dimensionless factor used to determine the equivalent dose from the absorbed dose averaged over a tissue or organ based on the type of radiation absorbed. The resulting weighted dose was designated as the organ- or tissue equivalent dose:
An equivalent dose of one rem represents that quantity of radiation dose that is equivalent to specified biological damage to one rad of X-rays or gamma rays. A dose of one rem caused by gamma radiation equals an energy deposition of one hundred ergs of energy in a kilogram of tissue. That means one rem is equivalent to one rad of gamma rays deposited in certain tissue. On the other hand, similar biological damage (one rem) can be caused only by 1/20 rad of alpha radiation (due to high wR of alpha radiation). Similarly, as for sieverts, rems are not a physical dose unit. For example, an absorbed dose of 1 rad by alpha particles will lead to an equivalent dose of 20 rems. This may seem to be a paradox. It implies that the energy of the incident radiation field in ergs has increased by a factor of 20, thereby violating the laws of Conservation of energy. However, this is not the case. The rem is derived from the physical quantity absorbed dose but also considers the biological effectiveness of the radiation, which is dependent on the radiation type and energy. The radiation weighting factor causes that the rem cannot be a physical unit.
One rem is also a large amount of equivalent dose. A person who has absorbed a whole-body dose of 1 rem has absorbed one hundred ergs of energy in each kg of body tissue (in case of gamma rays).
Equivalent doses measured in industry and medicine often have usually lower doses than one rem, and the following multiples are often used:
1 mrem (millirem) = 1E-3 rem
1 krem (kilorem) = 1E3 rem
Conversions from the SI units to other units are as follows:
- 1 Sv = 100 rem
- 1 mSv = 100 mrem
Radiation Weighting Factors – ICRP
For photon and electron radiation, the radiation weighting factor has the value of 1 independently of the energy of the radiation, and for alpha radiation, the value is 20. For neutron radiation, the value is energy-dependent and amounts to 5 to 20.

In 2007 ICRP published a new set of radiation weighting factors (ICRP Publ. 103: The 2007 Recommendations of the International Commission on Radiological Protection). These factors are given below.
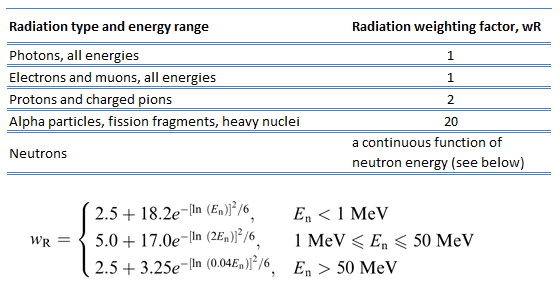
As shown in the table, a wR of 1 is for all low-LET radiations, i.e., X-rays and gamma rays of all energies as well as electrons and muons. A smooth curve, considered an approximation, was fitted to the wR values as a function of incident neutron energy. Note that En is the neutron energy in MeV.
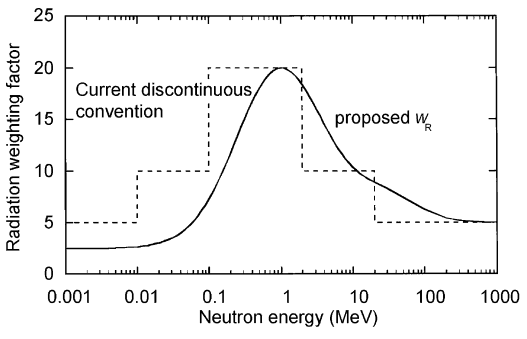
Thus, for example, an absorbed dose of 1 rad by alpha particles will lead to an equivalent dose of 20 rem, and an equivalent dose of radiation is estimated to have the same biological effect as an equal amount of absorbed dose of gamma rays, which is given a weighting factor of 1.
See also: Quality Factor
Examples of Doses in rems
We must note that radiation is all around us. In, around, and above the world we live in. It is a natural energy force that surrounds us, and it is a part of our natural world that has been here since the birth of our planet. In the following points, we try to express enormous ranges of radiation exposure, which can be obtained from various sources.
- 0.005 mrem – Sleeping next to someone
- 0.009 mrem – Living within 30 miles of a nuclear power plant for a year
- 0.01 mrem – Eating one banana
- 0.03 mrem – Living within 50 miles of a coal power plant for a year
- 1 mrem – Average daily dose received from natural background
- 2 mrem – Chest X-ray
- 4 mrem – A 5-hour airplane flight
- 60 mrem – mammogram
- 100 mrem – Dose limit for individual members of the public, total effective dose per annum
- 365 mrem – Average yearly dose received from natural background
- 580 mrem – Chest CT scan
- 1 000 mrem – Average yearly dose received from a natural background in Ramsar, Iran
- 2 000 mrem – single full-body CT scan
- 17 500 mrem – annual dose from natural radiation on a monazite beach near Guarapari, Brazil.
- 500 000 mrem – Dose that kills a human with a 50% risk within 30 days (LD50/30) if the dose is received over a very short duration.
As can be seen, low-level doses are common in everyday life. The previous examples can help illustrate relative magnitudes. From biological consequences, it is very important to distinguish between doses received over short and extended periods. An “acute dose” occurs over a short and finite period, while a “chronic dose” is a dose that continues for an extended period so that a dose rate better describes it. High doses tend to kill cells, while low doses tend to damage or change them. Low doses spread out over long periods don’t cause an immediate problem to any body organ. The effects of low radiation doses occur at the cell level, and the results may not be observed for many years.
Calculation of Shielded Dose Rate in rems
Assume the point isotropic source contains 1.0 Ci of 137Cs and has a half-life of 30.2 years. Note that the relationship between half-life and the amount of a radionuclide required to give an activity of one curie is shown below. This amount of material can be calculated using λ, which is the decay constant of certain nuclide:
About 94.6 percent decays by beta emission to a metastable nuclear isomer of barium: barium-137m. The main photon peak of Ba-137m is 662 keV. For this calculation, assume that all decays go through this channel.
Calculate the primary photon dose rate, in gray per hour (Gy.h-1), at the outer surface of a 5 cm thick lead shield. Then calculate the equivalent dose rate in sieverts and rems. Assume that this external radiation field penetrates uniformly through the whole body. The primary photon dose rate neglects all secondary particles. Assume that the effective distance of the source from the dose point is 10 cm. We shall also assume that the dose point is soft tissue and it can reasonably be simulated by water, and we use the mass-energy absorption coefficient for water.
See also: Gamma Ray Attenuation
See also: Shielding of Gamma Rays
Solution:
The primary photon dose rate is attenuated exponentially, and the dose rate from primary photons, taking account of the shield, is given by:
As can be seen, we do not account for the buildup of secondary radiation. If secondary particles are produced, or the primary radiation changes its energy or direction, the effective attenuation will be much less. This assumption generally underestimates the true dose rate, especially for thick shields and when the dose point is close to the shield surface, but this assumption simplifies all calculations. For this case, the true dose rate (with the buildup of secondary radiation) will be more than two times higher.
To calculate the absorbed dose rate, we have to use the formula:
- k = 5.76 x 10-7
- S = 3.7 x 1010 s-1
- E = 0.662 MeV
- μt/ρ = 0.0326 cm2/g (values are available at NIST)
- μ = 1.289 cm-1 (values are available at NIST)
- D = 5 cm
- r = 10 cm
Result:
The resulting absorbed dose rate in grays per hour is then:
Since the radiation weighting factor for gamma rays is equal to one, and we have assumed the uniform radiation field, we can directly calculate the equivalent dose rate from the absorbed dose rate as:
If we want to account for the buildup of secondary radiation, then we have to include the buildup factor. The extended formula for the dose rate is then:
——–