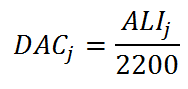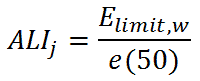Concentrations of radioactive materials in the air are limited by the Derived Air Concentration (DAC), which is derived from the ALI. The DAC is the activity concentration in air in units of Bq/m3 of the radionuclide considered, which would lead to an intake of an ALI (Bq) assuming a gender-averaged breathing rate of 1.1 m3/h and an annual working time of 2000 h (an annual air intake of 2200 m3).
The DAC was defined in by the ICRP in Publication 60 (ICRP, 1991b, paragraph S30) as:
“Derived air concentration equals the annual limit on intake, ALI, (of a radionuclide) divided by the volume of air inhaled by a Reference Person in a working year (i.e., 2.2×103 m3). The unit of DAC is Bq/m3.”
Special Reference: ICRP, 2007. The 2007 Recommendations of the International Commission on Radiological Protection. ICRP Publication 103. Ann. ICRP 37 (2-4).
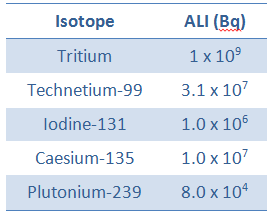
Therefore, if we divide the ALI by 2200 m3, we will get the DAC in Bq/m3. For example, the ALI of iodine-131 is 1 x 106 Bq. The corresponding DAC will be 1 000 000/2400 = 417 Bq/m3.
The DAC of radionuclide j is given by:
If a worker breathes air containing radioactive material at a concentration of 1 DAC for one hour, then the worker has been exposed to 1 DAC.hr.
See also: Airborne Contamination
Annual Limit on Intake – ALI
In assessing committed effective doses for workers, intakes of radioactive material are controlled by the Annual Limit on Intake (ALI) defined by the ICRP and expressed in units of activity (becquerels or curies).
The ALI was defined in by the ICRP in Publication 60 (ICRP, 1991b, paragraph S30) as:
“the activity intake (Bq) of a radionuclide which would lead to an effective dose corresponding to the annual limit Elimit;w, under the expectation that the worker is exposed to only this radionuclide.”
The ALI of radionuclide j is then:
where e(50) is the corresponding reference committed effective dose coefficient in (Sv/Bq). This dose coefficient, e(T), is determined by the radiotoxicity of a nuclide, and it accounts for radiation and tissue weighting factors and metabolic and biokinetic information.
See also: ICRP, 1994. Dose Coefficients for Intakes of Radionuclides by Workers. ICRP Publication 68. Ann. ICRP 24 (4).
The Commission recommended in Publication 60 that the ALI should be based on the dose limit of Elimit;w = 0.020 Sv in a year, with no time averaging. For members of the public, Elimit;w = 0.001 Sv is the recommended value.
As an example, let’s assume an intake of radioactive tritium. For tritium, the annual limit intake (ALI) is 1 x 109 Bq. If you take 1 x 109 Bq of tritium, you will receive a whole-body dose of 20 mSv. Note that the biological half-life is about 10 days, while the radioactive half-life is about 12 years. Instead of years, it takes a couple of months until the tritium has been pretty well eliminated. The committed effective dose, E(t), is 20 mSv. It does not depend on whether a person intakes this amount of activity in a short or long time. In every case, this person gets the same whole-body dose of 20 mSv.
For 131I, ICRP has calculated that if you inhale 1 x 106 Bq (ALI for 131I), you will receive a thyroid dose of HT = 400 mSv (and a weighted whole-body dose of 20 mSv).
Occupational Exposure – Effective Dose
In most situations of occupational exposure, the effective dose, E, can be derived from operational quantities using the following formula:
The committed dose is a dose quantity that measures the stochastic health risk due to an intake of radioactive material into the human body. Since the operational dose limit of 20 mSv applies to the sum of the internal and external exposures, if a worker has some external dose, the ALI must be modified or offset to account for the external dose. For example, assume the worker has 10 mSv from external radiation sources, and only 10 more mSv are allowed from internal radiation before the worker reaches the occupational whole body limit.
See also: Dose Limits