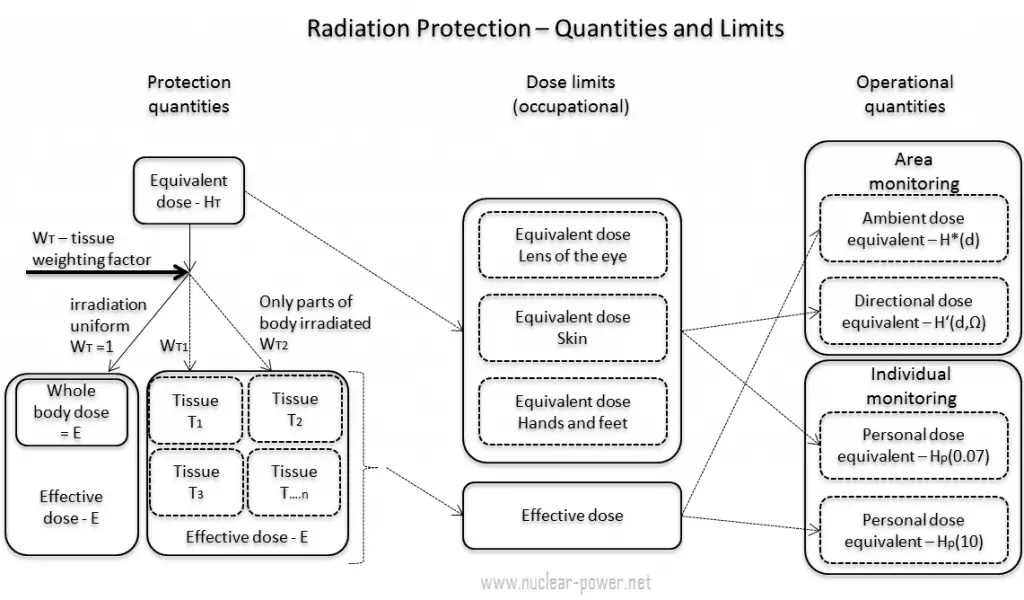
The directional dose equivalent is an operational quantity for area monitoring weakly penetrating radiation. The directional dose equivalent, H’ (d, Ω), is the operational quantity for the determination of equivalent dose to the skin, lens of the eye, etc., also for beta radiation and low-energy photons.
According to the ICRP, the directional dose equivalent is defined as:
ICRP Publication 103:
“The dose equivalent at a point in a radiation field that would be produced by the corresponding expanded field in the ICRU sphere at a depth, d, on a radius in a specified direction, Ω.”
The directional dose equivalent is given the symbol H’ (0.07, Ω) or, in rare cases, H’ (3, Ω). The SI unit of H’ (d, Ω) is the sievert (Sv). Unit of sievert was named after the Swedish scientist Rolf Sievert, who did a lot of the early work on dosimetry in radiation therapy. For all types of external radiation, the operational quantities for area monitoring are defined based on an equivalent dose value at a point in a simple phantom, the ICRU sphere, which is a sphere of tissue-equivalent material (30 cm in diameter, ICRU (soft) tissue with density: 1 g/cm3, and mass composition: 76.2% oxygen, 11.1% carbon, 10.1% hydrogen, and 2.6% nitrogen).
As was written, operational quantities are measurable, unlike an effective dose, and instruments for radiation monitoring are calibrated in terms of these quantities. In monitoring, the values of these operational quantities are taken as a sufficiently precise assessment of effective dose and skin dose, respectively, if their values are below the protection limits. Numerical links between operational quantities and effective dose are represented by conservative conversion coefficients, which are defined for a reference person.
Dose Limits
See also: Dose Limits
Dose limits are split into two groups, the public and occupationally exposed workers. According to ICRP, occupational exposure refers to all exposure incurred by workers in the course of their work, except for
- excluded exposures and exposures from exempt activities involving radiation or exempt sources
- any medical exposure
- the normal local natural background radiation.
The following table summarizes dose limits for occupationally exposed workers and the public:
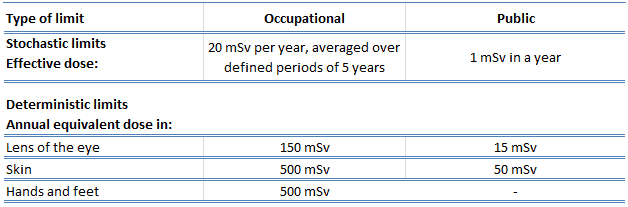
Source of data: ICRP, 2007. The 2007 Recommendations of the International Commission on Radiological Protection. ICRP Publication 103. Ann. ICRP 37 (2-4).
According to the recommendation of the ICRP in its statement on tissue reactions of 21. April 2011, the equivalent dose limit for the eye lens for occupational exposure in planned exposure situations was reduced from 150 mSv/year to 20 mSv/year, averaged over defined periods of 5 years, with no annual dose in a single year exceeding 50 mSv.
Limits on effective dose are for the sum of the relevant, effective doses from external exposure in the specified period and the committed effective dose from intakes of radionuclides in the same period. For adults, the committed effective dose is computed for a 50-year period after intake, whereas for children, it is computed for the period up to age 70. The effective whole-body dose limit of 20 mSv is an average value over five years, and the real limit is 100 mSv in 5 years, with not more than 50 mSv in any year.
Occupational Exposure – Effective Dose
In most situations of occupational exposure, the effective dose, E, can be derived from operational quantities using the following formula:
The committed dose is a dose quantity that measures the stochastic health risk due to an intake of radioactive material into the human body.
