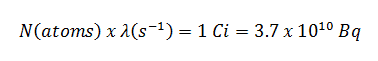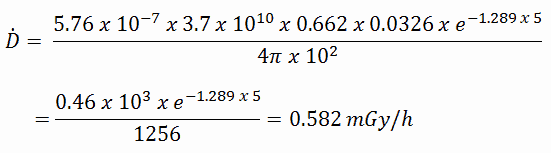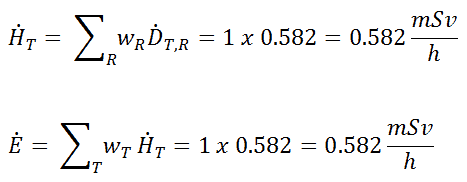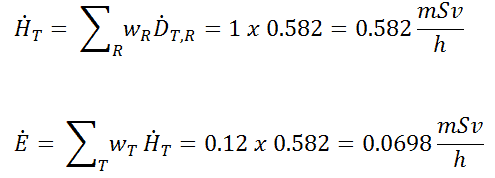Surface contamination means that radioactive material has been deposited on surfaces (such as walls and floors). It may be loosely deposited, much like ordinary dust, or firmly fixed by a chemical reaction. This distinction is important, and we classify surface contamination based on how easily it can be removed:
- Free Contamination. In the case of free contamination (or loose contamination), the radioactive material can be spread. This is surface contamination that can easily be removed with simple decontamination methods. For example, if dust particles containing various radioisotopes land on the person’s skin or garments, we can clean it up or remove clothes. Once a person has decontaminated, all particulate radioactivity sources are eliminated, and the individual is no longer contaminated. Free contamination is also a more serious hazard than fixed contamination because dust particles can become airborne and easily ingested, and this leads to internal exposure to radioactive contaminants. Although almost all contaminants are beta radioactive with accompanying gamma emission, there is also the possibility of alpha contamination in any nuclear fuel handling areas.
- Fixed Contamination. In the case of fixed contamination, the radioactive material cannot be spread since it is chemically or mechanically bound to structures. It cannot be removed by normal cleaning methods. Fixed contamination is a less serious hazard than free contamination and cannot be re-suspended or transferred to the skin. Therefore the hazard is usually an external one only. On the other hand, it depends on the level of contamination. Although almost all contaminants are beta radioactive with accompanying gamma emission, there is also the possibility of alpha contamination in any nuclear fuel handling areas. Unless the level of contamination is very severe, the gamma radiation dose rate will be small and external exposure will be significant only in contact with, or very close to, the contaminated surfaces. Since beta particles are less penetrating than gamma rays, the beta dose rate can be high only at contact. A value of 1 mSv/h at contact for a contamination level of 400 – 500 Bq/cm2 is fairly representative.
Calculation of Shielded Dose Rate in Sieverts from Contaminated Surface
Assume a surface that is contaminated by 1.0 Ci of 137Cs. Assume that this contaminant can be approximated by the point isotropic source, which contains 1.0 Ci of 137Cs, and has a half-life of 30.2 years. Note that the relationship between half-life and the amount of a radionuclide required to give an activity of one curie is shown below. This amount of material can be calculated using λ, which is the decay constant of certain nuclide:
About 94.6 percent decays by beta emission to a metastable nuclear isomer of barium: barium-137m. The main photon peak of Ba-137m is 662 keV. For this calculation, assume that all decays go through this channel.
Calculate the primary photon dose rate, in sieverts per hour (Sv.h-1), at the outer surface of a 5 cm thick lead shield. Then calculate the equivalent and effective dose rates for two cases.
- Assume that this external radiation field penetrates uniformly through the whole body. That means: Calculating the effective whole-body dose rate.
- Assume that this external radiation field penetrates only the lungs, and the other organs are completely shielded. That means: Calculating the effective dose rate.
Note that the primary photon dose rate neglects all secondary particles. Assume that the effective distance of the source from the dose point is 10 cm. We shall also assume that the dose point is soft tissue and it can reasonably be simulated by water, and we use the mass-energy absorption coefficient for water.
See also: Gamma Ray Attenuation
See also: Shielding of Gamma Rays
Solution:
The primary photon dose rate is attenuated exponentially, and the dose rate from primary photons, taking account of the shield, is given by:
As can be seen, we do not account for the buildup of secondary radiation. If secondary particles are produced, or the primary radiation changes its energy or direction, the effective attenuation will be much less. This assumption generally underestimates the true dose rate, especially for thick shields and when the dose point is close to the shield surface, but this assumption simplifies all calculations. For this case, the true dose rate (with the buildup of secondary radiation) will be more than two times higher.
To calculate the absorbed dose rate, we have to use the formula:
- k = 5.76 x 10-7
- S = 3.7 x 1010 s-1
- E = 0.662 MeV
- μt/ρ = 0.0326 cm2/g (values are available at NIST)
- μ = 1.289 cm-1 (values are available at NIST)
- D = 5 cm
- r = 10 cm
Result:
The resulting absorbed dose rate in grays per hour is then:
1) Uniform irradiation
Since the radiation weighting factor for gamma rays is equal to one, and we have assumed the uniform radiation field (the tissue weighting factor is also equal to unity), we can directly calculate the equivalent dose rate and the effective dose rate (E = HT) from the absorbed dose rate as:
2) Partial irradiation
In this case, we assume partial irradiation of the lungs only. Thus, we have to use the tissue weighting factor equal to wT = 0.12. The radiation weighting factor for gamma rays is equal to one. As a result, we can calculate the effective dose rate as:
If one part of the body (e.g., the lungs) receives a radiation dose, it represents a risk for a particularly damaging effect (e.g., lung cancer). The same dose given to another organ represents a different risk factor.
If we want to account for the buildup of secondary radiation, then we have to include the buildup factor. The extended formula for the dose rate is then:
——–