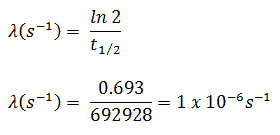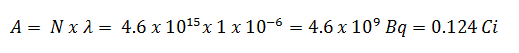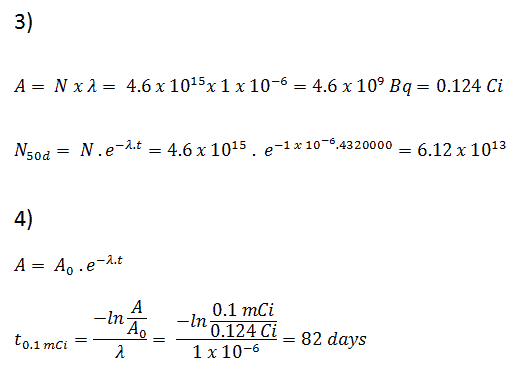Facebook Instagram Youtube Twitter

Curie to Becquerel – Conversion – Calculation

The original unit for measuring the amount of radioactivity was the curie (symbol Ci), a non-SI unit of radioactivity defined in 1910. A curie was originally named in honor of Pierre Curie but was considered at least by some to be in honor of Marie Curie as well. A curie was originally defined as equivalent to the number of disintegrations that one gram of radium-226 will undergo in one second. Currently, a curie is defined as 1Ci = 3.7 x 1010 disintegrations per second. Therefore:

1Ci = 3.7 x 1010 Bq = 37 GBq

The SI unit for measuring the amount of radioactivity is the becquerel (symbol Bq). The becquerel is named in honour of Henri Becquerel, a French physicist who discovered radioactivity in 1896. One becquerel (1Bq) is equal to 1 disintegration per second.

Curie to Becquerel – Problem with Solution

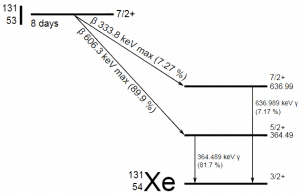Iodine 131 - decay schemeA sample of material contains 1 microgram of iodine-131. Note that iodine-131 plays a major role as a radioactive isotope present in nuclear fission products. It is a major contributor to health hazards when released into the atmosphere during an accident. Iodine-131 has a half-life of 8.02 days.

Calculate:

  1. The number of iodine-131 atoms is initially present.
  2. The activity of the iodine-131 in curies.
  3. The number of iodine-131 atoms will remain in 50 days.
  4. The time it will take for the activity to reach 0.1 mCi.

Solution:

  1. The number of atoms of iodine-131 can be determined using isotopic mass as below.

NI-131 = mI-131 . NA / MI-131

NI-131 = (1 μg) x (6.02×1023 nuclei/mol) / (130.91 g/mol)

NI-131 = 4.6 x 1015 nuclei

  1. The activity of the iodine-131 in curies can be determined using its decay constant:

The iodine-131 has a half-life of 8.02 days (692928 sec), and therefore its decay constant is:

Using this value for the decay constant, we can determine the activity of the sample:

3) and 4) The number of iodine-131 atoms that will remain in 50 days (N50d) and the time it will take for the activity to reach 0.1 mCi can be calculated using the decay law:

As can be seen, after 50 days, the number of iodine-131 atoms and thus the activity will be about 75 times lower. After 82 days, the activity will be approximately 1200 times lower. Therefore, the time of ten half-lives (factor 210 = 1024) is widely used to define residual activity.

References:

Radiation Protection:

  1. Knoll, Glenn F., Radiation Detection and Measurement 4th Edition, Wiley, 8/2010. ISBN-13: 978-0470131480.
  2. Stabin, Michael G., Radiation Protection and Dosimetry: An Introduction to Health Physics, Springer, 10/2010. ISBN-13: 978-1441923912.
  3. Martin, James E., Physics for Radiation Protection 3rd Edition, Wiley-VCH, 4/2013. ISBN-13: 978-3527411764.
  4. U.S.NRC, NUCLEAR REACTOR CONCEPTS
  5. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Nuclear and Reactor Physics:

  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
  9. Paul Reuss, Neutron Physics. EDP Sciences, 2008. ISBN: 978-2759800414.

See above:

Units of Radioactivity