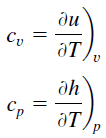Article Summary & FAQs
What is the ideal gas law?
According to the ideal gas law, pressure varies linearly with temperature and quantity and inversely with volume. The ideal gas law is utilized by engineers working with gases because it is simple and approximates real gas behavior.
Key Facts
What is an ideal gas:
An ideal gas is defined as one in which all collisions between atoms or molecules are perfectly elastic and in which there are no attractive intermolecular forces.
Ideal gas model:
The ideal gas model is used to predict the behavior of gases and is one of the most useful and commonly used substance models ever developed. It was found that if we confine 1 mol samples of various gases in identical volumes and hold the gases at the same temperature, their measured pressures are almost the same.
Equation of state:
Any equation that relates the pressure, temperature and specific volume of a substance is called an equation of state. The simplest and best-known equation of state for substances in the gas phase is the Ideal Gas equation of state.
pV = nRT
where:
- p is the absolute pressure of the gas
- n is the amount of substance
- T is the absolute temperature
- V is the volume
- R is the ideal, or universal, gas constant, equal to the product of the Boltzmann constant and the Avogadro constant,
In this equation, the symbol R is the universal gas constant with the same value for all gases—namely, R = 8.31 J/mol K.
Gas laws:
Émile Clapeyron first stated the ideal gas equation in 1834 as a combination of these laws:
Internal energy:
For diatomic ideal gas:
Eint = 5/2 NkT = 5/2 nRT
Validity of the ideal gas law:
The ideal gas law is accurate only at relatively low pressures (relative to the critical pressure pcr) and high temperatures (relative to the critical temperature Tcr).
Ideal Gas Law
Any equation that relates the pressure, temperature and specific volume of a substance is called an equation of state. The simplest and best-known equation of state for substances in the gas phase is the Ideal Gas equation of state. Émile Clapeyron first stated it in 1834 as a combination of the empirical Boyle’s law, Charles’ law, and Avogadro’s Law. This equation predicts the p-v-T behavior of gas quite accurately for dilute or low-pressure gases. In an ideal gas, molecules have no volume and do not interact. According to the ideal gas law, pressure varies linearly with temperature and quantity and inversely with volume.
pV = nRT
where:
- p is the absolute pressure of the gas
- n is the amount of substance
- T is the absolute temperature
- V is the volume
- R is the ideal, or universal, gas constant, equal to the product of the Boltzmann constant and the Avogadro constant,
In this equation, the symbol R is the universal gas constant with the same value for all gases—namely, R = 8.31 J/mol K.
The power of the ideal gas law is in its simplicity. When any two thermodynamic variables, p, v, and T, are given, the third can easily be found. Many physical conditions of gases calculated by engineers fit the above description. Perhaps the most common use of gas behavior studied by engineers is that of the compression process and expansion process using ideal gas approximations.
What is an Ideal Gas
An ideal gas is defined as one in which all collisions between atoms or molecules are perfectly elastic and in which there are no attractive intermolecular forces. An ideal gas can be visualized as a collection of perfectly hard spheres that collide but otherwise do not interact. In reality, no real gases are like an ideal gas, and therefore no real gases follow the ideal gas law or equation completely. At temperatures near a gases boiling point, increases in pressure will cause condensation and drastic decreases in volume. At very high pressures, the intermolecular forces of gas are significant. However, most gases are in approximate agreement at pressures and temperatures above their boiling point. The ideal gas law is utilized by engineers working with gases because it is simple and approximates real gas behavior.
See also: Elastic Collision
Ideal Gas Model
The ideal gas model is used to predict the behavior of gases and is one of the most useful and commonly used substance models ever developed. It was found that if we confine 1 mol samples of various gases in identical volumes and hold the gases at the same temperature, then their measured pressures are almost the same. Moreover, when we confine gases at lower densities, the differences tend to disappear. It was found, such gases tend to obey the following relation, which is known as the ideal gas law:
pV = nRT
where:
p is the absolute pressure of the gas
n is the amount of substance
T is the absolute temperature
V is the volume
R is the ideal, or universal, gas constant, equal to the product of the Boltzmann constant and the Avogadro constant. The power of the ideal gas law is in its simplicity. When any two thermodynamic variables, p, v, and T, are given, the third can easily be found.
The ideal gas model is based on the following assumptions:
- The pressure, volume, and temperature of an ideal gas obey the ideal gas law.
- The specific internal energy is only a function of the temperature: u = u(T).
- The molar mass of an ideal gas is identical to the molar mass of the real substance.
- The specific heats — cp and cv — are independent of temperature, which means constants.
From the microscopic point of view, it is based on these assumptions:
- The molecules of the gas are small, hard spheres.
- The only forces between the gas molecules are those that determine the point-like collisions.
- All collisions are elastic, and all motion is frictionless.
- The average distance between molecules is much larger than the size of the molecules.
- The molecules are moving in random directions.
- There is no other attractive or repulsive force between these molecules.
Joule’s Second Law
For any gas whose equation of state is given exactly by pV = nRT (or pv = RT), the specific internal energy depends on temperature only. This rule was originally found in 1843 by an English physicist James Prescott Joule experimentally for real gases and is known as Joule’s second law:
The internal energy of a fixed mass of an ideal gas depends only on its temperature (not pressure or volume).
The specific enthalpy of a gas described by pV = nRT also depends on temperature only. Note that enthalpy is the thermodynamic quantity equivalent to the total heat content of a system. It is equal to the internal energy of the system plus the product of pressure and volume. In intensive variables the Joule’s second law is therefore given by h = h(T) = u(T) + pv = u(T) + RT.
These three equations constitute the ideal gas model, summarized as follows:
pv = RT
u = u(T)
h = h(T) = u(T) + RT
Gas Laws
In general, the gas laws are the first equations of state that correlate densities of gases and liquids to temperatures and pressures. The gas laws were completely developed at the end of the 18th century. These laws or statements preceded the ideal gas law since, individually, these laws are considered as special cases of the ideal gas equation, with one or more of the variables held constant. Since they have been almost completely replaced by the ideal gas equation, it is not usual for students to learn these laws in detail. Émile Clapeyron first stated the ideal gas equation in 1834 as a combination of these laws:
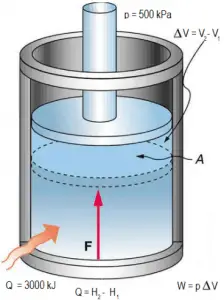
Example: Ideal Gas Law – Gas compression inside a pressurizer

Pressure in the primary circuit of PWRs is maintained by a pressurizer, a separate vessel connected to the primary circuit (hot leg), and partially filled with water heated to the saturation temperature (boiling point) for the desired pressure by submerged electrical heaters. During the plant heat up, the pressurizer can be filled with nitrogen instead of saturated steam.
Assume that a pressurizer contains 12 m3 of nitrogen at 20°C and 15 bar. The temperature is raised to 35°C, and the volume is reduced to 8.5 m3. What is the final pressure of the gas inside the pressurizer? Assume that the gas is ideal.
Solution:
Since the gas is ideal, we can use the ideal gas law to relate its parameters, both in the initial state i and in the final state f. Therefore:
pinitVinit = nRTinit
and
pfinalVfinal = nRTfinal
Dividing the second equation by the first equation and solving for pf we obtain:
pfinal = pinitTfinalVinit / TinitVfinal
Note that we cannot convert units of volume and pressure to basic SI units because they cancel out each other. On the other hand, we have to use Kelvins instead of degrees of Celsius. Therefore Tinit = 293 K and Tfinal = 308 K.
It follows, the resulting pressure in the final state will be:
pfinal = (15 bar) x (308 K) x (12 m3) / (293 K) x (8.5 m3) = 22 bar
Validity of Ideal Gas Law
Since ideal gas is defined as one in which all collisions between atoms or molecules are perfectly elastic. There are no attractive intermolecular forces, and there is no such thing in nature as a truly ideal gas. On the other hand, all real gases approach the ideal state at low pressures (densities). At low pressures, molecules are far enough apart that they do not interact with one another.
In other words, the Ideal Gas Law is accurate only at relatively low pressures (relative to the critical pressure pcr) and high temperatures (relative to the critical temperature Tcr). At these parameters, the compressibility factor, Z = pv / RT, is approximately 1. The compressibility factor is used to account for deviation from the ideal situation. This correction factor is dependent on pressure and temperature for each gas considered.
Internal Energy of an Ideal Gas
The internal energy is the total of all the energy associated with the motion of the atoms or molecules in the system. Microscopic forms of energy include those due to the rotation, vibration, translation, and interactions among the molecules of a substance.[/lgc_column]
Monatomic Gas – Internal Energy
For a monatomic ideal gas (such as helium, neon, or argon), the only contribution to the energy comes from translational kinetic energy. The average translational kinetic energy of a single atom depends only on the gas temperature and is given by the equation:
Kavg = 3/2 kT.
The internal energy of n moles of an ideal monatomic (one atom per molecule) gas is equal to the average kinetic energy per molecule times the total number of molecules, N:
Eint = 3/2 NkT = 3/2 nRT
where n is the number of moles, each direction (x, y, and z) contributes (1/2)nRT to the internal energy. This is where the equipartition of energy idea comes in – any other contribution to the energy must also contribute (1/2)nRT. As can be seen, the internal energy of an ideal gas depends only on temperature and the number of moles of gas.
Diatomic Molecule – Internal Energy
If the gas molecules contain more than one atom, there are three translation directions, and rotational kinetic energy contributes, but only for rotations about two of the three perpendicular axes. The five contributions to the energy (five degrees of freedom) give:
Diatomic ideal gas:
Eint = 5/2 NkT = 5/2 nRT
This is only an approximation and applies at intermediate temperatures. Only the translational kinetic energy contributes at low temperatures, and at higher temperatures, two additional contributions (kinetic and potential energy) come from vibration. The internal energy will be greater at a given temperature than for a monatomic gas, but it will still function only as temperature for an ideal gas.
The internal energy of real gases also depends mainly on temperature. Still, similarly to the Ideal Gas Law, real gases’ internal energy also depends somewhat on pressure and volume. All real gases approach the ideal state at low pressures (densities). At low pressures, molecules are far enough apart that they do not interact with one another. The internal energy of liquids and solids is quite complicated, for it includes electrical potential energy associated with the forces (or chemical bonds) between atoms and molecules.
Specific Heat at Constant Volume and Constant Pressure
Specific heat is a property related to internal energy that is very important in thermodynamics. The intensive properties cv and cp are defined for pure, simple compressible substances as partial derivatives of the internal energy u(T, v) and enthalpy h(T, p), respectively:
where the subscripts v and p denote the variables held fixed during differentiation. The properties cv and cp are referred to as specific heats (or heat capacities). Under certain special conditions, they relate the temperature change to the amount of energy added by heat transfer. Their SI units are J/kg K, or J/mol K. Two specific heats are defined for gases, constant volume (cv), and constant pressure (cp).
 According to the first law of thermodynamics, for a constant volume process with a monatomic ideal gas, the molar specific heat will be:
According to the first law of thermodynamics, for a constant volume process with a monatomic ideal gas, the molar specific heat will be:
Cv = 3/2R = 12.5 J/mol K
because
U = 3/2nRT
It can be derived that the molar specific heat at constant pressure is:
Cp = Cv + R = 5/2R = 20.8 J/mol K
This Cp is greater than the molar specific heat at constant volume Cv, because energy must now be supplied not only to raise the temperature of the gas but also for the gas to do work. In this case, volume changes.
Mayer’s relation – Mayer’s formula
Julius Robert Mayer, a German chemist, and physicist derived a relation between specific heat at constant pressure and the specific heat at constant volume for an ideal gas. He studied the fact that the specific heat capacity at constant pressure (Cp) is slightly greater than at constant volume (Cv). He reasoned that this Cp is greater than the molar specific heat at constant volume Cv, because energy must now be supplied not only to raise the temperature of the gas but also for the gas to do work. In this case, volume changes. According to Mayer’s relation or Mayer’s formula, the difference between these two heat capacities is equal to the universal gas constant. Thus the molar specific heat at constant pressure is equal:
Cp = Cv + R