In general, the gas laws are the first equations of state that correlate densities of gases and liquids to temperatures and pressures. The gas laws were completely developed at the end of the 18th century. These laws or statements preceded the ideal gas law since, individually, these laws are considered as special cases of the ideal gas equation, with one or more of the variables held constant. Since they have been almost completely replaced by the ideal gas equation, it is not usual for students to learn these laws in detail. The ideal gas equation was first stated by Émile Clapeyron in 1834 as a combination of these laws:
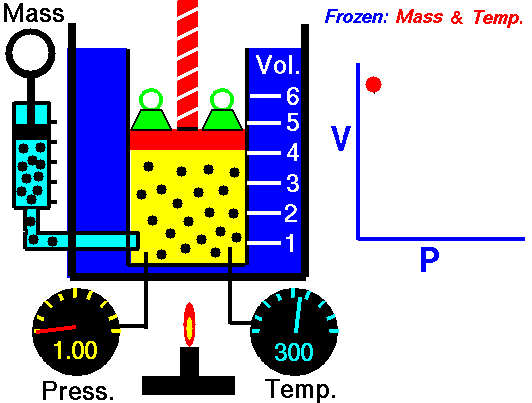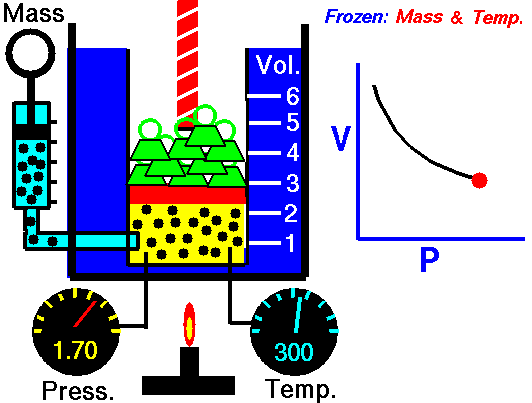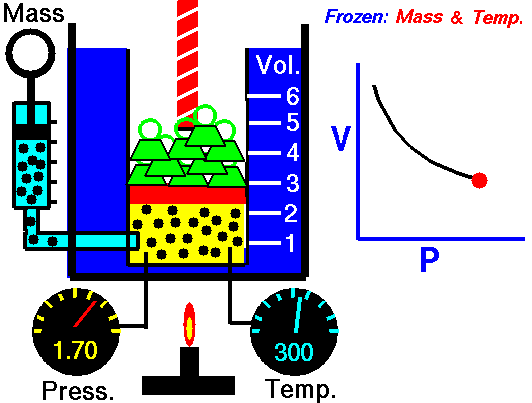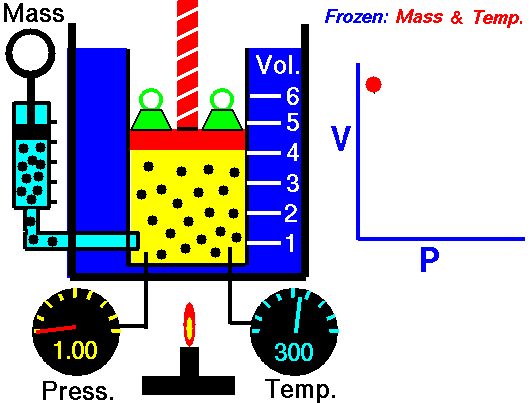
Boyle-Mariotte Law
Boyle-Mariotte Law is one of the gas laws. At the end of the 17th century, Robert William Boyle and Edme Mariotte independently studied the relationship between the volume and pressure of a gas at a constant temperature. Certain experiments with gases at relatively low pressure led Robert Boyle to formulate a well-known law. It states that:
For a fixed mass of gas at a constant temperature, the volume is inversely proportional to the pressure.
That means that, for example, if you increase the volume 10 times, the pressure will decrease 10 times. If you halve the volume, you will double the pressure.
You can express this mathematically as:
pV = constant
or
p1V1 = p2V2
Yes, it seems to be identical to the isothermal process of an ideal gas. In fact, during their experiments, the temperature remained constant, as was assumed by Mariotte. These results are fully consistent with the ideal gas law, which determinates that the constant is equal to nRT.
pV = nRT
where:
- p is the absolute pressure of the gas
- n is the amount of substance
- T is the absolute temperature
- V is the volume
- R is the ideal, or universal, gas constant, equal to the product of the Boltzmann constant and the Avogadro constant,
In this equation the symbol R is a constant called the universal gas constant that has the same value for all gases—namely, R = 8.31 J/mol K.
Charles’s Law
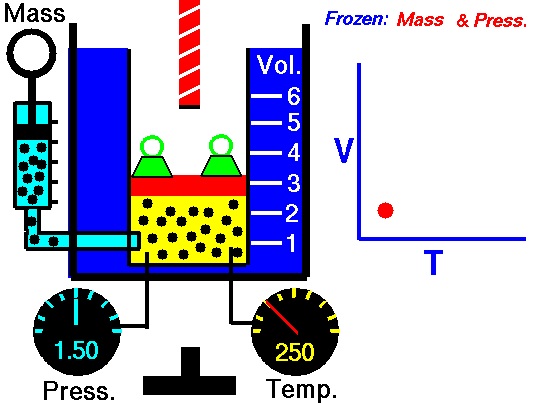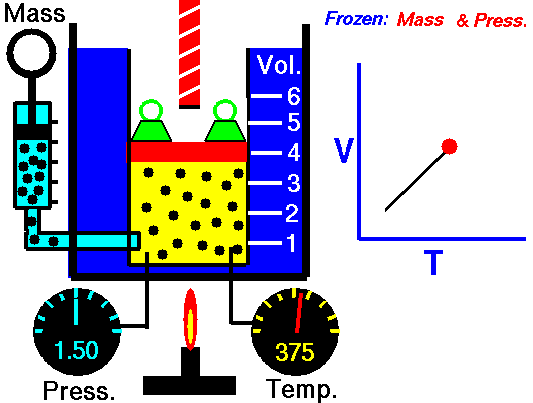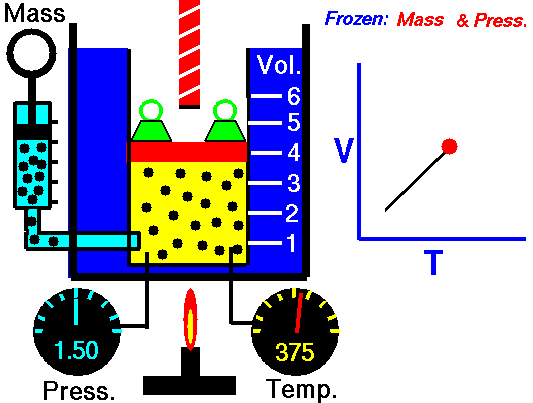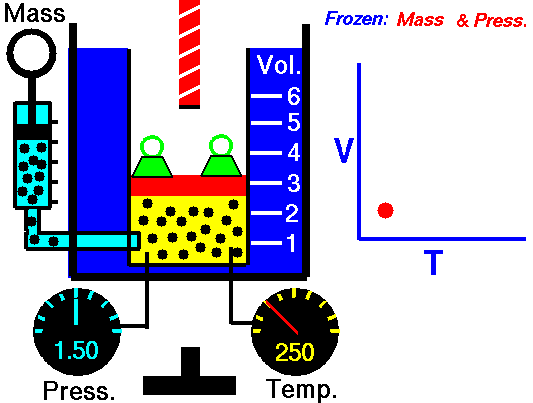
Charles’s Law is one of the gas laws. At the end of the 18th century, a French inventor and scientist, Jacques Alexandre César Charles, studied the relationship between the volume and the temperature of a gas at constant pressure. The results of certain experiments with gases at relatively low pressure led Jacques Alexandre César Charles to formulate a well-known law. It states that:
For a fixed mass of gas at constant pressure, the volume is directly proportional to the Kelvin temperature.
That means that, for example, if you double the temperature, you will double the volume. If you halve the temperature, you will halve the volume.
You can express this mathematically as:
V = constant . T
Yes, it seems to be identical to the isobaric process of an ideal gas. These results are fully consistent with the ideal gas law, which determinates that the constant is equal to nR/p. If you rearrange the pV = nRT equation by dividing both sides by p, you will obtain:
V = nR/p . T
where nR/p is constant and:
- p is the absolute pressure of the gas
- n is the amount of substance
- T is the absolute temperature
- V is the volume
- R is the ideal, or universal, gas constant, equal to the product of the Boltzmann constant and the Avogadro constant,
In this equation the symbol R is a constant called the universal gas constant that has the same value for all gases—namely, R = 8.31 J/mol K.
Guy-Lussac’s Law
Guy-Lussac’s Law or the Pressure Law is one of the gas laws. In the late 18th and early 19th centuries, it was discovered by French chemist Joseph Louis Gay-Lussac. He studied the relationship between the pressure and the temperature of a gas at constant volume. The results of certain experiments with gases at relatively low pressure led Joseph Louis Gay-Lussac to formulate a well-known “Pressure Law”. It states that:
For a fixed mass of gas at constant volume, the pressure is directly proportional to the Kelvin temperature.
That means that, for example, if you double the temperature, you will double the pressure. If you halve the temperature, you will halve the pressure.
You can express this mathematically as:
p = constant . T
Yes, it seems to be identical to the isochoric process of an ideal gas. These results are fully consistent with the ideal gas law, which determinates that the constant is equal to nR/V. If you rearrange the pV = nRT equation by dividing both sides by V, you will obtain:
p = nR/V . T
where nR/V is constant and:
- p is the absolute pressure of the gas
- n is the amount of substance
- T is the absolute temperature
- V is the volume
- R is the ideal, or universal, gas constant, equal to the product of the Boltzmann constant and the Avogadro constant,
In this equation, the symbol R is a constant called the universal gas constant that has the same value for all gases—namely, R = 8.31 J/mol K.
Avogadro’s Law
Avogadro’s Law is one of the gas laws. At the beginning of the 19th century, Italian scientist Lorenzo Romano Amedeo Carlo Avogadro studied the relationship between the volume and the amount of gas present. The results of certain experiments with gases led him to formulate a well-known Avogadro’s Law. It states that, under the same conditions of temperature and pressure, equal volumes of different gases contain an equal number of molecules, or:
For a fixed mass of an ideal gas at constant pressure and temperature, the volume and amount of the gas are directly proportional.
You can express this mathematically as:
V ∝ n
or
V = constant . n
where nR/V is constant and:
- n is the amount of substance measured in moles
- V is the volume of the gas
the constant is equal is to RT/p, where p is the absolute pressure of the gas, T is the absolute temperature, and R is the ideal, or universal, gas constant, equal to the product of the Boltzmann constant and the Avogadro constant.
Avogadro’s Number
In tribute to Avogadro, also the number of particles (atoms, molecules, ions, or other particles) in 1 mole of a substance, 6.022×1023, was named after Avogadro as the Avogadro constant or Avogadro number. The Avogadro constant is one of the seven SI base units and is represented by NA.
The Avogadro’s Law can be used for comparing the same substance under two different sets of conditions:
V1 / n1 = V2 / n2
Molar Volume of Gases
One of the most practical results of this law is the molar volume of a gas, Vm, which is about:
Vm = 22.4 dm3 / mol
It means, at standard temperature (273.15 K, 0°C) and standard atmospheric pressure (101.325 kPa), the molar volume is the same for all ideal gases. Note that it is under the ideal gas assumption. This value is strongly dependent on the pressure and the temperature. For example:
- for 273.15 K (0°C) and 100.00 kPa, the molar volume of an ideal gas is 22.71 dm3.mol−1
- for 298.15 K (25°C) and 100.00 kPa, the molar volume of an ideal gas is 24.79 dm3.mol−1