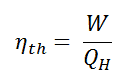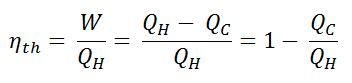Four laws of thermodynamics define fundamental physical quantities (temperature, energy, and entropy) and characterize thermodynamic systems at thermal equilibrium. These are considered as one of the most important laws in all of physics. The laws are as follows:
If two systems are both in thermal equilibrium with a third, then they are in thermal equilibrium with each other.
This law provides a definition and method of defining temperatures, perhaps the most important intensive property of a system when dealing with thermal energy conversion problems.
The first law of thermodynamics:
The increase in internal energy of a closed system is equal to the heat supplied to the system minus work done by it.
This law is the principle of conservation of energy. It is the most important law for analyzing most systems and quantifying how thermal energy is transformed to other forms of energy. It follows perpetual motion machines of the first kind are impossible.
The second law of thermodynamics:
The entropy of any isolated system never decreases. In a natural thermodynamic process, the sum of the entropies of the interacting thermodynamic systems increases.
This law indicates the irreversibility of natural processes. Reversible processes are a useful and convenient theoretical fiction but do not occur in nature. From this law, it is impossible to construct a device that operates on a cycle and whose sole effect is the transfer of heat from a cooler body to a hotter body. It follows perpetual motion machines of the second kind are impossible.
The third law of thermodynamics:
The entropy of a system approaches a constant value as the temperature approaches absolute zero.
Based on empirical evidence, this law states that the entropy of a pure crystalline substance is zero at the absolute zero of temperature, 0 K and that it is impossible using any process, no matter how idealized, to reduce the temperature of a system to absolute zero in a finite number of steps. This allows us to define a zero point for the thermal energy of a body.
Popular Version of the Laws of Thermodynamics
0. You must play the game.
1. You can’t win; you can only break even.
2. You can only break even at absolute zero.
3. You can’t reach absolute zero.
Heat in Thermodynamics
See also: Heat in Thermodynamics
While internal energy refers to the total energy of all the molecules within the object, heat is the amount of energy flowing spontaneously from one body to another due to their temperature difference. Heat is a form of energy, but it is energy in transit. Heat is not a property of a system. However, the transfer of energy as heat occurs at the molecular level due to a temperature difference.
Consider a metal block at high temperature that consists of atoms oscillating intensely around their average positions. At low temperatures, the atoms continue to oscillate but with less intensity. If a hotter block of metal is put in contact with a cooler block, the intensely oscillating atoms at the edge of the hotter block give off their kinetic energy to the less oscillating atoms at the edge of the cool block. In this case, there is energy transfer between these two blocks, and heat flows from the hotter to the cooler block by these random vibrations.
In general, when two objects are brought into thermal contact, heat will flow between them until they come into equilibrium with each other. When a temperature difference does exist, heat flows spontaneously from the warmer system to the colder system. Heat transfer occurs by conduction or by thermal radiation. When the flow of heat stops, they are said to be at the same temperature. They are then said to be in thermal equilibrium.
As with work, the amount of heat transferred depends upon the path and not simply on the initial and final conditions of the system. There are many ways to take the gas from state i to state f.
Also, as with work, it is important to distinguish between heat added to a system from its surroundings and heat removed from a system to its surroundings. Q is positive for heat added to the system, so Q is negative if heat leaves the system. Because W in the equation is the work done by the system, then if work is done on the system, W will be negative, and Eint will increase.
The symbol q is sometimes used to indicate the heat added to or removed from a system per unit mass. It equals the total heat (Q) added or removed divided by the mass (m).
Work in Thermodynamics
See also: Work in Thermodynamics
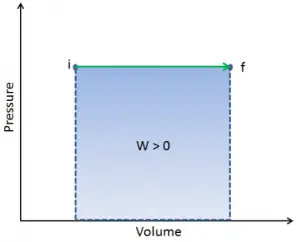
In thermodynamics, work performed by a system is the energy transferred by the system to its surroundings. Kinetic energy, potential energy, and internal energy are forms of energy that are properties of a system. Work is a form of energy, but it is energy in transit. A system contains no work, and work is a process done by or on a system. In general, work is defined for mechanical systems as the action of a force on an object through a distance.
W = F . d
where:
W = work (J)
F = force (N)
d = displacement (m)
Heat Engines
Energy sources have always played a very important role in the development of human society. Energy is generally defined as the potential to do work or produce heat. Sometimes it is like the “currency” for performing work. One of the most wonderful properties of the universe is that energy can be transformed from one type to another and transferred from one object to another.
In general, it is easy to produce thermal energy by doing work, for example, by any frictional process. But to get work from thermal energy is more difficult. It is closely associated with the concept of entropy. For example, electricity is particularly useful since it has very low entropy (is highly ordered) and can be converted into other forms of energy very efficiently.
Sometimes, mechanical energy is directly available, for example, wind power and hydropower. But most of our energy comes from burning fossil fuels (coal, oil, and gas) and nuclear reactions. At present, fossil fuel is still the world’s predominant energy source. But the burning of fossil fuels generates only thermal energy. Therefore these energy sources are so-called “primary energy sources” that must be converted to the secondary energy source, so-called energy carriers (electrical energy, etc.). A heat engine must be used to convert thermal energy into another form of energy.
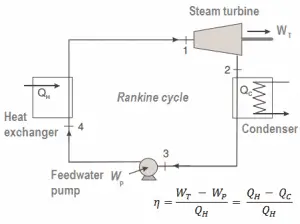
In general, a heat engine is a device that converts chemical energy to heat or thermal energy and then to mechanical energy or electrical energy. Many heat engines operate cyclically, adding energy in the form of heat in one part of the cycle and using that energy to do useful work in another part of the cycle.
For example, as is typical in all conventional thermal power plants, the heat is used to generate steam which drives a steam turbine connected to a generator that produces electricity. Steam generators, steam turbines, condensers, and feedwater pumps constitute a heat engine subject to the efficiency limitations imposed by the second law of thermodynamics. In modern nuclear power plants, the overall thermodynamic efficiency is about one-third (33%), so 3000 MWth of thermal power from the fission reaction is needed to generate 1000 MWe of electrical power.
See also: Heat Engines
Thermal Efficiency
We define the thermal efficiency, ηth, of any heat engine as the ratio of the work it does, W, to the heat input at the high temperature, QH.
The thermal efficiency, ηth, represents the fraction of heat, QH, converted to work. It is a dimensionless performance measure of a heat engine that uses thermal energy, such as a steam turbine, an internal combustion engine, or a refrigerator. For refrigeration or heat pumps, thermal efficiency indicates the extent to which the energy added by work is converted to net heat output. Since it is a dimensionless number, we must always express W, QH, and QC in the same units.
Since energy is conserved according to the first law of thermodynamics and energy cannot be converted to work completely, the heat input, QH, must equal the work done, W, plus the heat that must be dissipated as waste heat QC into the environment. Therefore we can rewrite the formula for thermal efficiency as:
To give the efficiency as a percent, we multiply the previous formula by 100. Note that ηth could be 100% only if the waste heat QC is zero.
In general, the efficiency of even the best heat engines is quite low. In short, it isn’t easy to convert thermal energy to mechanical energy. The thermal efficiencies are usually below 50% and often far below. Be careful when comparing it with efficiencies of wind or hydropower (wind turbines are not heat engines). There is no energy conversion between thermal and mechanical energy.
See also: Carnot’s Principle
See also: Thermal Efficiency