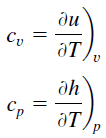 Different substances are affected to different magnitudes by the addition of heat. When a given amount of heat is added to different substances, their temperatures increase by different amounts. This proportionality constant between the heat Q that the object absorbs or loses and the resulting temperature change T of the object is known as the heat capacity C of an object.
Different substances are affected to different magnitudes by the addition of heat. When a given amount of heat is added to different substances, their temperatures increase by different amounts. This proportionality constant between the heat Q that the object absorbs or loses and the resulting temperature change T of the object is known as the heat capacity C of an object.
C = Q / ΔT
Heat capacity is an extensive property of matter, meaning it is proportional to the size of the system. Heat capacity C has the unit of energy per degree or energy per kelvin. When expressing the same phenomenon as an intensive property, the heat capacity is divided by the amount of substance, mass, or volume. Thus the quantity is independent of the size or extent of the sample.
Specific Heat Capacity
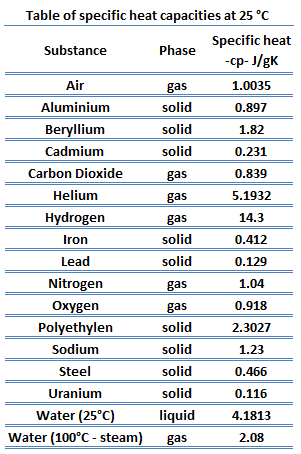
The heat capacity of a substance per unit mass is called the substance’s specific heat capacity (cp). The subscript p indicates that the heat capacity and specific heat capacity apply when the heat is added or removed at constant pressure.
cp = Q / mΔT
Specific Heat Capacity of Ideal Gas
In the Ideal Gas Model, the intensive properties cv and cp are defined for pure, simple compressible substances as partial derivatives of the internal energy u(T, v) and enthalpy h(T, p), respectively:
where the subscripts v and p denote the variables held fixed during differentiation. The properties cv and cp are referred to as specific heats (or heat capacities). Under certain special conditions, they relate the temperature change of a system to the amount of energy added by heat transfer. Their SI units are J/kg K, or J/mol K. Two specific heats are defined for gases, constant volume (cv), and constant pressure (cp).
 According to the first law of thermodynamics, for a constant volume process with a monatomic ideal gas, the molar specific heat will be:
According to the first law of thermodynamics, for a constant volume process with a monatomic ideal gas, the molar specific heat will be:
Cv = 3/2R = 12.5 J/mol K
because
U = 3/2nRT
It can be derived that the molar specific heat at constant pressure is:
Cp = Cv + R = 5/2R = 20.8 J/mol K
This Cp is greater than the molar specific heat at constant volume Cv, because energy must now be supplied not only to raise the temperature of the gas but also for the gas to do work because in this case volume changes.