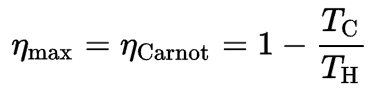In 1824, a French engineer and physicist, Nicolas Léonard Sadi Carnot, advanced the study of the second law by forming a principle (also called Carnot’s rule) that specifies limits on the maximum efficiency any heat engine can obtain. In short, this principle states that the efficiency of a thermodynamic cycle depends solely on the difference between the hot and cold temperature reservoirs.
Carnot’s principle states:
- No engine can be more efficient than a reversible engine (Carnot heat engine) operating between the same high-temperature and low-temperature reservoirs.
- The efficiencies of all reversible engines (Carnot heat engines) operating between the same constant temperature reservoirs are the same, regardless of the working substance employed or the operation details.
Carnot Efficiency
The formula for this maximum efficiency is:
where:
- is the efficiency of the Carnot cycle, i.e., it is the ratio = W/QH of the work done by the engine to the heat energy entering the system from the hot reservoir.
- TC is the absolute temperature (Kelvins) of the cold reservoir,
- TH is the absolute temperature (Kelvins) of the hot reservoir.
Example: Carnot efficiency for coal-fired power plant
In a modern coal-fired power plant, the temperature of high pressure steam (Thot) would be about 400°C (673K) and Tcold, the cooling tower water temperature, would be about 20°C (293K). For this type of power plant the maximum (ideal) efficiency will be:
= 1 – Tcold/Thot = 1 – 293/673 = 56%
It must be added, and this is an idealized efficiency. The Carnot efficiency is valid for reversible processes. These processes cannot be achieved in real cycles of power plants. The Carnot efficiency dictates that higher efficiencies can be attained by increasing the temperature of the steam. This feature is also valid for real thermodynamic cycles. But this requires an increase in pressures inside boilers or steam generators. However, metallurgical considerations place upper limits on such pressures. Sub-critical fossil fuel power plants which operate under critical pressure (i.e., lower than 22.1 MPa) can achieve 36–40% efficiency. Supercritical designs operated at supercritical pressure (i.e., greater than 22.1 MPa) have efficiencies of around 43%. Most efficient and complex coal-fired power plants operated at “ultra critical” pressures (i.e., around 30 MPa) and used multiple-stage reheat reach about 48% efficiency.
See also: Supercritical Reactor
Causes of Inefficiency
As was discussed, an efficiency can range between 0 and 1. Each heat engine is somehow inefficient. This inefficiency can be attributed to three causes.
- Irreversibility of Processes. There is an overall theoretical upper limit to the efficiency of conversion of heat to work in any heat engine. This upper limit is called the Carnot efficiency. According to the Carnot principle, no engine can be more efficient than a reversible engine (Carnot heat engine) operating between the same high temperature and low-temperature reservoirs. For example, when the hot reservoir has Thot of 400°C (673K) and Tcold of about 20°C (293K), the maximum (ideal) efficiency will be: = 1 – Tcold/Thot = 1 – 293/673 = 56%. But all real thermodynamic processes are somehow irreversible. They are not done infinitely slowly. Therefore, heat engines must have lower efficiencies than limits on their efficiency due to the inherent irreversibility of the heat engine cycle they use.
- Presence of Friction and Heat Losses. In real thermodynamic systems or real heat engines, a part of the overall cycle inefficiency is due to the losses by the individual components. In real devices (such as turbines, pumps, and compressors), mechanical friction, heat losses, and losses in the combustion process cause further efficiency losses.
- Design Inefficiency. Finally, the last and important source of inefficiencies is the compromises made by engineers when designing a heat engine (e.g.,, power plant). They must consider cost and other factors in the design and operation of the cycle. As an example, consider the design of the condenser in the thermal power plants. Ideally, the steam exhausted into the condenser would have no subcooling. But real condensers are designed to subcool the liquid by a few degrees Celsius to avoid the suction cavitation in the condensate pumps. But, this subcooling increases the inefficiency of the cycle because more energy is needed to reheat the water.