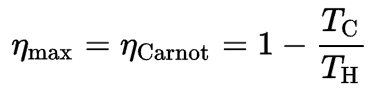Kelvin-Planck Statement of the Second Law:
“It is impossible to construct a device which operates on a cycle and produces no other effect than the production of work and the transfer of heat from a single body”.
This statement operates with the term “thermal reservoir” or “single reservoir”. A reservoir is a large object in which the temperature remains constant while energy is extracted. Such a system can be approximated in many ways—by the earth’s atmosphere, large bodies of water like lakes, oceans, and so on.
The Kelvin–Planck statement does not exclude the existence of a system that develops a net amount of work from a heat transfer extracted from a thermal reservoir. According to this statement, a system undergoing a cycle cannot develop a positive net amount of work from a heat transfer extracted from a thermal reservoir.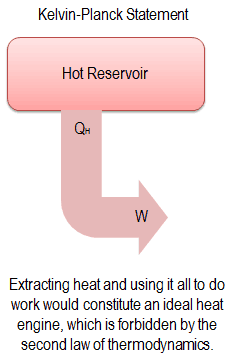
Various Statements of the Law
The second law of thermodynamics may be expressed in many specific ways. Each statement expresses the same law. Listed below are three that are often encountered.
Before these statements, we have to remind the French engineer and physicist, Nicolas Léonard Sadi Carnot, advanced the study of the second law by forming a principle (also called Carnot’s rule) that specifies limits on the maximum efficiency of any heat engine can obtain.
Carnot’s Principle
In 1824, a French engineer and physicist,
Nicolas Léonard Sadi Carnot, advanced the study of the second law by forming a principle (also called
Carnot’s rule) that specifies limits on the
maximum efficiency any heat engine can obtain. In short, this principle states that the
efficiency of a thermodynamic cycle depends solely on the difference between the hot and cold temperature reservoirs.
Carnot’s principle states:
- No engine can be more efficient than a reversible engine (Carnot heat engine) operating between the same high-temperature and low-temperature reservoirs.
- The efficiencies of all reversible engines (Carnot heat engines) operating between the same constant temperature reservoirs are the same, regardless of the working substance employed or the operation details.
Carnot Efficiency
The formula for this maximum efficiency is:
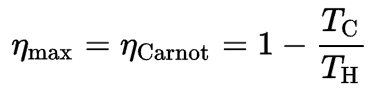
where:
- is the efficiency of the Carnot cycle, i.e., it is the ratio = W/QH of the work done by the engine to the heat energy entering the system from the hot reservoir.
- TC is the absolute temperature (Kelvins) of the cold reservoir,
- TH is the absolute temperature (Kelvins) of the hot reservoir.
Spoiler title
In a modern
coal-fired power plant, the temperature of
high-pressure steam (T
hot) would be about 400°C (673K) and T
cold, the cooling tower water temperature, would be about 20°C (293K). For this type of power plant, the maximum (ideal) efficiency will be:
= 1 – Tcold/Thot = 1 – 293/673 = 56%
It must be added. This is an idealized efficiency. The Carnot efficiency is valid for reversible processes. These processes cannot be achieved in real cycles of power plants. The Carnot efficiency dictates that higher efficiencies can be attained by increasing the temperature of the steam. This feature is also valid for real thermodynamic cycles. But this requires an increase in pressures inside boilers or steam generators. However, metallurgical considerations place upper limits on such pressures. Sub-critical fossil fuel power plants under critical pressure (i.e., lower than 22.1 MPa) can achieve 36–40% efficiency. Supercritical designs operated at supercritical pressure (i.e., greater than 22.1 MPa) have efficiencies of around 43%. Most efficient and complex coal-fired power plants operate at “ultra critical” pressures (i.e., around 30 MPa) and use multiple stage reheat to reach about 48% efficiency.
See also: Supercritical Reactor
References:
Nuclear and Reactor Physics:
- J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
- J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
- W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
- Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
- W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
- Kenneth S. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN: 978-0471805533
- G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
- Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
- U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.
Advanced Reactor Physics:
- K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
- K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
- D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
- E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.