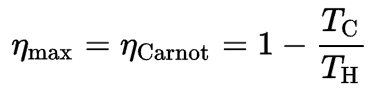According to the third law of thermodynamics:
The entropy of a system approaches a constant value as the temperature approaches absolute zero.
Based on empirical evidence, this law states that the entropy of a pure crystalline substance is zero at the absolute zero of temperature, 0 K and that it is impossible using any process, no matter how idealized, to reduce the temperature of a system to absolute zero in a finite number of steps. This allows us to define a zero point for the thermal energy of a body.
The German chemist Walther Nernst developed the third law of thermodynamics during the years 1906–12. For this research, Walther Nernst won the 1920 Nobel Prize in chemistry. Therefore the third law of thermodynamics is often referred to as Nernst’s theorem or Nernst’s postulate. As can be seen, the third law of thermodynamics states that the entropy of a system in thermodynamic equilibrium approaches zero as the temperature approaches zero. Or conversely, the absolute temperature of any pure crystalline substance in thermodynamic equilibrium approaches zero when the entropy approaches zero.
Nernst Heat Theorem (a consequence of the Third Law) is:
It is impossible for any process, no matter how idealized, to reduce the entropy of a system to its absolute-zero value in a finite number of operations.
Mathematically:
German physicist Max Planck later used the Nernst heat theorem to define the third law of thermodynamics in terms of entropy and absolute zero.
Some materials (e.g.,, any amorphous solid) do not have a well-defined order at absolute zero. In these materials (e.g.,, glass), some finite entropy also remains at absolute zero because the system’s microscopic structure (atom by atom) can be arranged in different ways (W ≠ 1). This constant entropy is known as the residual entropy, which is the difference between a non-equilibrium state and the crystal state of a substance close to absolute zero.
Note that the exact definition of entropy is:
Entropy = (Boltzmann’s constant k) x logarithm of the number of possible states
S = kB logW
This equation, which relates the microscopic details, or microstates, of the system (via W) to its macroscopic state (via the entropy S), is the key idea of statistical mechanics.
Absolute Zero
Absolute zero is the coldest theoretical temperature, at which the thermal motion of atoms and molecules reaches its minimum. This is a state at which the enthalpy and entropy of a cooled ideal gas reach its minimum value, taken as 0.
Mathematically:
lim ST→0 = 0
where
S = entropy (J/K)
T = absolute temperature (K)
Classically, this would be a state of motionlessness, but quantum uncertainty dictates that the particles still possess finite zero-point energy. Absolute zero is denoted as 0 K on the Kelvin scale, −273.15 °C on the Celsius scale, and −459.67 °F on the Fahrenheit scale.
Relation to Heat Engines
According to Carnot’s principle, which specifies limits on the maximum efficiency any heat engine can have is the Carnot efficiency. This principle also states that the efficiency of a Carnot cycle depends solely on the difference between the hot and cold temperature reservoirs.
where:
- is the efficiency of the Carnot cycle, i.e., it is the ratio = W/QH of the work done by the engine to the heat energy entering the system from the hot reservoir.
- TC is the absolute temperature (Kelvins) of the cold reservoir,
- TH is the absolute temperature (Kelvins) of the hot reservoir,
The third law dictates that TC can never be zero. Therefore we see that a 100% efficient heat engine is not possible.