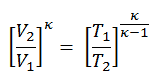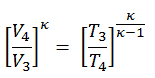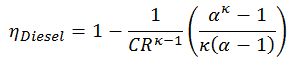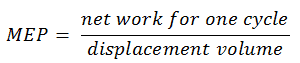Let assume the Diesel cycle, which is one of the most common thermodynamic cycles that can be found in automobile engines. One of the key parameters of such engines is the change in volumes between the top dead center (TDC) to bottom dead center (BDC). The ratio of these volumes (V1 / V2) is known as the compression ratio. Also, the cut-off ratio is V3/V2, which is the ratio of volumes at the end and start of the combustion phase.
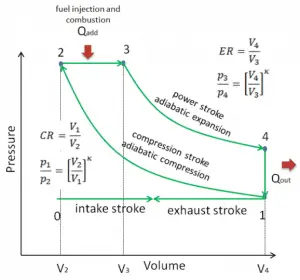
lIn this example, let us assume the Diesel cycle with a compression ratio of CR = 20 : 1 and cut-off ratio α = 2. The air is at 100 kPa = 1 bar, 20 °C (293 K), and the chamber volume is 500 cm³ before the compression stroke.
- Specific heat capacity at a constant air pressure at atmospheric pressure and room temperature: cp = 1.01 kJ/kgK.
- Specific heat capacity at constant air volume at atmospheric pressure and room temperature: cv = 0.718 kJ/kgK.
- κ = cp/cv = 1.4
Calculate:
- the mass of intake air
- the temperature T2
- the pressure p2
- the temperature T3
- the amount of heat added by burning of fuel-air mixture
- the thermal efficiency of this cycle
- the MEP
Solution:
1)
At the beginning of calculations, we must determine the amount of gas in the cylinder before the compression stroke. Using the ideal gas law, we can find the mass:
pV = mRspecificT
where:
- p is the absolute pressure of the gas
- m is the mass of the substance
- T is the absolute temperature
- V is the volume
- Rspecific is the specific gas constant, equal to the universal gas constant divided by the gas or mixture’s molar mass (M). For dry air Rspecific = 287.1 J.kg-1.K-1.
Therefore
m = p1V1/RspecificT1 = (100000 × 500×10-6 )/(287.1 × 293) = 5.95×10-4 kg
2)
In this problem all volumes are known:
- V1 = V4 = Vmax = 500×10-6 m3 (0.5l)
- V2 = Vmin = Vmax / CR = 25 ×10-6 m3
Note that (Vmax – Vmin) x number of cylinders = total engine displacement
Since the process is adiabatic, we can use the following p, V, T relation for adiabatic processes:
thus
T2 = T1 . CRκ – 1 = 293 . 200.4 = 971 K
3)
Again, we can use the ideal gas law to find the pressure at the end of the compression stroke as:
p2 = mRspecificT2 / V2 = 5.95×10-4 x 287.1 x 971 / 25 ×10-6 = 6635000 Pa = 66.35 bar
4)
Since process 2 → 3 occurs at constant pressure, the ideal gas equation of state gives
T3 = (V3/V2) x T2 = 1942 K
To calculate the amount of heat added by burning of fuel-air mixture, Qadd, we have to use the first law of thermodynamics for the isobaric process, which states:
Qadd = mcp (T3 – T2) = 5.95×10-4 x 1010 x 971 = 583.5 J
5)
Thermal efficiency for this Diesel cycle:
As was derived in the previous section, the thermal efficiency of the Diesel cycle is a function of the compression ratio, the cut-off ratio, and κ:
- ηDiesel is the maximum thermal efficiency of a Diesel cycle
- α is the cut-off ratio V3/V2 (i.e., the ratio of volumes at the end and start of the combustion phase)
- CR is the compression ratio
- κ = cp/cv = 1.4
For this example:
ηDiesel = 0.6467 = 64.7%
6)
The MEP was defined as:
It this equation the displacement volume is equal to Vmax – Vmin. The net work for one cycle can be calculated using the heat added and the thermal efficiency:
Wnet = Qadd . ηOtto = 583.5 x 0.6467 = 377.3 J
MEP = 377.3 / (500×10-6 – 25 ×10-6) = 794.3 kPa = 7.943 bar