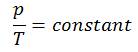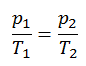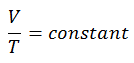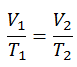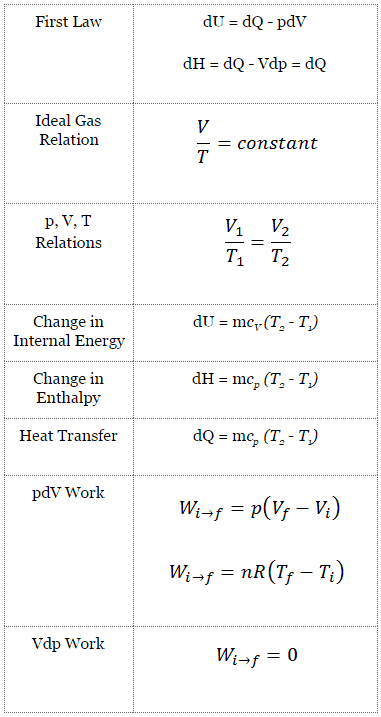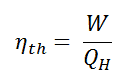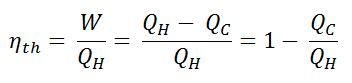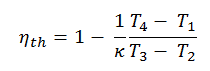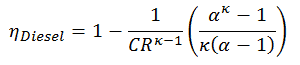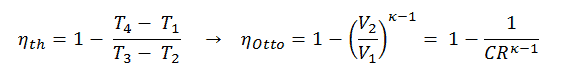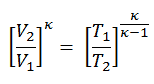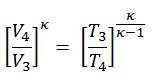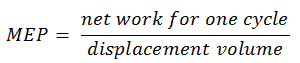In the 1890s, a German inventor, Rudolf Diesel has patented his invention of an efficient, slow-burning, compression ignition, internal combustion engine. The original cycle proposed by Rudolf Diesel was a constant temperature cycle. In later years Diesel realized his original cycle would not work, and he adopted the constant pressure cycle, which is known as the Diesel cycle.
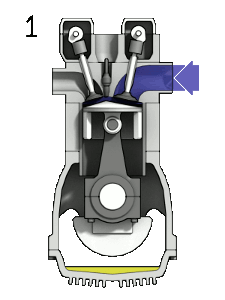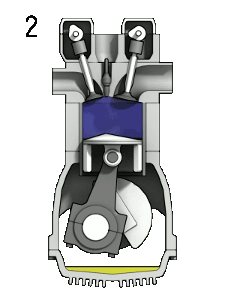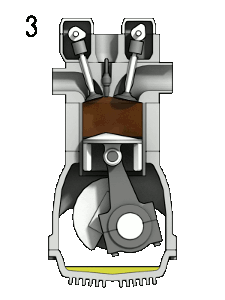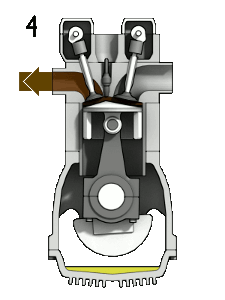
The diesel cycle is one of the most common thermodynamic cycles found in automobile engines and describes the functioning of a typical compression ignition piston engine. The Diesel engine is similar in operation to the gasoline engine. The most important difference is that:
- There is no fuel in the cylinder at the beginning of the compression stroke. Therefore autoignition does not occur in Diesel engines.
- A diesel engine uses compression ignition instead of spark ignition.
- Because of the high temperature developed during the adiabatic compression, the fuel spontaneously ignites as it is injected. Therefore no spark plugs are needed.
- Before the beginning of the power stroke, the injectors start to inject fuel directly into the combustion chamber. Therefore the first part of power stroke occurs approximately at the constant pressure.
- Higher compression ratios can be achieved in Diesel engines than in Otto engines.
Since Carnot’s principle states that no engine can be more efficient than a reversible engine (a Carnot heat engine) operating between the same high temperature and low-temperature reservoirs, the Diesel engine must have lower efficiency than the Carnot efficiency. A typical diesel automotive engine operates at around 30% to 35% of thermal efficiency. About 65-70% is rejected as waste heat without being converted into useful work, i.e., work delivered to wheels. In general, engines using the Diesel cycle are usually more efficient than engines using the Otto cycle. The diesel engine has the highest thermal efficiency of any practical combustion engine. Low-speed diesel engines (as used in ships) can have a thermal efficiency that exceeds 50%. The largest diesel engine in the world peaks at 51.7%.
Diesel Cycle – Processes
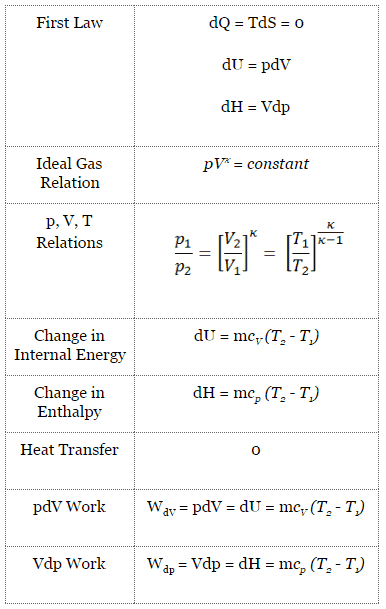
In an ideal Diesel cycle, the system executing the cycle undergoes a series of four processes: two isentropic (reversible adiabatic) processes alternated with one isochoric process and one isobaric process.
-
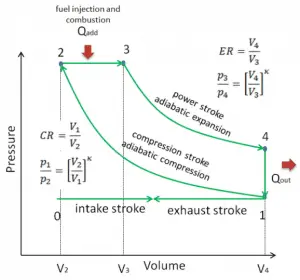
pV diagram of an ideal Diesel cycle Isentropic compression (compression stroke) – The air is compressed adiabatically from state 1 to state 2 as the piston moves from bottom dead center to top dead center. The surroundings do work on the gas, increasing its internal energy (temperature) and compressing it. On the other hand, the entropy remains unchanged. The changes in volumes and their ratio (V1 / V2) are known as the compression ratio.
- Isobaric expansion (ignition phase) – In this phase (between state 2 and state 3), there is a constant pressure (idealized model) heat transfer to the air from an external source (combustion of injected fuel) while the piston is moving toward the V3. During the constant pressure process, energy enters the system as heat Qadd, and a part of the work is done by moving pistons.
- Isentropic expansion (power stroke) – The gas expands adiabatically from state 3 to state 4 as the piston moves from V3 to the bottom dead center. The gas works on the surroundings (piston) and loses internal energy equal to the work that leaves the system. Again the entropy remains unchanged. The volume ratio (V4 / V3) is known as the isentropic expansion ratio.
- Isochoric decompression (exhaust stroke) – In this phase, the cycle completes by a constant-volume process in which heat is rejected from the air while the piston is at the bottom dead center. The working gas pressure drops instantaneously from point 4 to point 1. The exhaust valve opens at point 4. The exhaust stroke is directly after this decompression. As the piston moves from the bottom dead center (point 1) to the top dead center (point 0) with the exhaust valve opened, the gaseous mixture is vented to the atmosphere, and the process starts anew.
During the Diesel cycle, work is done on the gas by the piston between states 1 and 2 (isentropic compression). The gas works on the piston between stages 2 and 3 (isobaric heat addition) and stages 2 and 3 (isentropic expansion). The difference between the work done by the gas and the work done on the gas is the network produced by the cycle, and it corresponds to the area enclosed by the cycle curve. The work produced by the cycle times the rate of the cycle (cycles per second) is equal to the power produced by the Diesel engine.
Isentropic Process
An isentropic process is a thermodynamic process in which the entropy of the fluid or gas remains constant. It means the isentropic process is a special case of an adiabatic process in which there is no transfer of heat or matter. It is a reversible adiabatic process. The assumption of no heat transfer is very important since we can use the adiabatic approximation only in very rapid processes.
Isentropic Process and the First Law
For a closed system, we can write the first law of thermodynamics in terms of enthalpy:
dH = dQ + Vdp
or
dH = TdS + Vdp
Isentropic process (dQ = 0):
dH = Vdp → W = H2 – H1 → H2 – H1 = Cp (T2 – T1) (for ideal gas)
Isentropic Process of the Ideal Gas
The isentropic process (a special case of the adiabatic process) can be expressed with the ideal gas law as:
pVκ = constant
or
p1V1κ = p2V2κ
in which κ = cp/cv is the ratio of the specific heats (or heat capacities) for the gas. One for constant pressure (cp) and one for constant volume (cv). Note that, this ratio κ = cp/cv is a factor in determining the speed of sound in a gas and other adiabatic processes.
Isochoric Process
An isochoric process is a thermodynamic process in which the volume of the closed system remains constant (V = const). It describes the behavior of gas inside the container that cannot be deformed. Since the volume remains constant, the heat transfer into or out of the system does not the p∆V work but only changes the system’s internal energy (the temperature).
Isochoric Process and the First Law
The classical form of the first law of thermodynamics is the following equation:
dU = dQ – dW
In this equation, dW is equal to dW = pdV and is known as the boundary work. Then:
dU = dQ – pdV
An isochoric process and the ideal gas, all of the heat added to the system, will increase the internal energy.
Isochoric process (pdV = 0):
dU = dQ (for ideal gas)
dU = 0 = Q – W → W = Q (for ideal gas)
Isochoric Process of the Ideal Gas
The isochoric process can be expressed with the ideal gas law as:
or
On a p-V diagram, the process occurs along a horizontal line with the equation V = constant.
See also: Guy-Lussac’s Law.
Isobaric Process
An isobaric process is a thermodynamic process in which the system’s pressure remains constant (p = const). The heat transfer into or out of the system does work and changes the system’s internal energy.
Since there are changes in internal energy (dU) and changes in system volume (∆V), engineers often use the enthalpy of the system, which is defined as:
H = U + pV
Isobaric Process and the First Law
The classical form of the first law of thermodynamics is the following equation:
dU = dQ – dW
In this equation, dW is equal to dW = pdV and is known as the boundary work. In an isobaric process and the ideal gas, part of the heat added to the system will be used to do work, and part of the heat added will increase the internal energy (increase the temperature). Therefore it is convenient to use enthalpy instead of internal energy.
Isobaric process (Vdp = 0):
dH = dQ → Q = H2– H1
At constant entropy, i.e., in the isentropic process, the enthalpy change equals the flow process work done on or by the system.
Isobaric Process of the Ideal Gas
The isobaric process can be expressed with the ideal gas law as:
or
On a p-V diagram, the process occurs along a horizontal line (called an isobar) with the equation p = constant.
See also: Charles’s Law
Comparison of Actual and Ideal Diesel Cycles
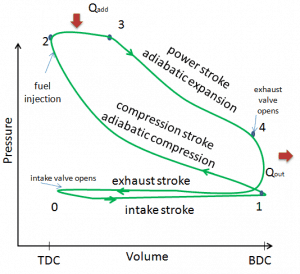 This article shows an ideal Diesel cycle in which there are a lot of assumptions that differ from the actual Diesel cycle. The main differences between the actual and ideal Diesel engines appear in the figure. In reality, the ideal cycle does not occur, and there are many losses associated with each process. For an actual cycle, the shape of the pV diagram is similar to the ideal, but the area (work) enclosed by the pV diagram is always less than the ideal value. The ideal Diesel cycle is based on the following assumptions:
This article shows an ideal Diesel cycle in which there are a lot of assumptions that differ from the actual Diesel cycle. The main differences between the actual and ideal Diesel engines appear in the figure. In reality, the ideal cycle does not occur, and there are many losses associated with each process. For an actual cycle, the shape of the pV diagram is similar to the ideal, but the area (work) enclosed by the pV diagram is always less than the ideal value. The ideal Diesel cycle is based on the following assumptions:
- Closed cycle: The largest difference between the two diagrams is the simplification of the intake and exhaust strokes in the ideal cycle. In the exhaust stroke, heat Qout is ejected into the environment (in a real engine, the gas leaves the engine and is replaced by a new mixture of air and fuel).
- Isobaric heat addition. In real engines, the heat addition is never isobaric.
- No heat transfer
- Compression – The gas is compressed adiabatically from state 1 to state 2. In real engines, there are always some inefficiencies that reduce the thermal efficiency.
- Expansion. The gas expands adiabatically from state 3 to state 4.
- Complete combustion of the mixture.
- No pumping work. Pumping work is the difference between the work done during the exhaust stroke and the intake stroke. In real cycles, there is a pressure difference between exhaust and inlet pressures.
- No blowdown loss. Blowdown loss is caused by the early opening of exhaust valves. This results in a loss of work output during the expansion stroke.
- No blow-by loss. The blow-by loss is caused by the leakage of compressed gases through piston rings and other crevices.
- No frictional losses.
These simplifying assumptions and losses lead to the fact that the enclosed area (work) of the pV diagram for an actual engine is significantly smaller than the area (work) enclosed by the pV diagram of the ideal cycle. In other words, the ideal engine cycle will overestimate the network and, if the engines run at the same speed, greater power is produced by the actual engine by around 20% (similarly as in the case of Otto engine).
Thermal Efficiency for Diesel Cycle
In general, the thermal efficiency, ηth, of any heat engine is defined as the ratio of the work it does, W, to the heat input at the high temperature, QH.
The thermal efficiency, ηth, represents the fraction of heat, QH, converted to work. Since energy is conserved according to the first law of thermodynamics and energy cannot be converted to work completely, the heat input, QH, must equal the work done, W, plus the heat that must be dissipated as waste heat QC into the environment. Therefore we can rewrite the formula for thermal efficiency as:
The heat absorbed occurs during combustion of fuel-air mixture, when the spark occurs, roughly at constant volume. Since during an isochoric process there is no work done by or on the system, the first law of thermodynamics dictates ∆U = ∆Q. Therefore, the heat added and rejected is given by:
Qadd = mcp (T3 – T2)
Qout = mcv (T4 – T1)
Substituting these expressions for the heat added and rejected in the expression for thermal efficiency yields:
This equation can be rearranged to the form with the compression ratio and the cut-off ratio:
where
- ηDiesel is the maximum thermal efficiency of a Diesel cycle
- α is the cut-off ratio V3/V2 (i.e., the ratio of volumes at the end and start of the combustion phase)
- CR is the compression ratio
- κ = cp/cv = 1.4
It is a very useful conclusion because it is desirable to achieve a high compression ratio to extract more mechanical energy from a given fuel mass. As concluded in the previous section, the air-standard Otto cycle thermal efficiency is also a function of compression ratio and κ.
When we compare these to formulae, it can be seen that the Otto cycle will be more efficient for a given compression ratio (CR) than the Diesel cycle. But diesel engines are usually more efficient since they can operate at higher compression ratios.
In ordinary Otto engines, the compression ratio has its limits. The compression ratio in a gasoline-powered engine will usually not be much higher than 10:1. Higher compression ratios will make gasoline engines subject to engine knocking, caused by the autoignition of an unburned mixture if lower octane-rated fuel is used. There is minimal risk of autoignition of the fuel because diesel engines are compression-ignition engines, and there is no fuel in the cylinder at the beginning of the compression stroke.
Diesel Cycle – Problem with Solution

Let assume the Diesel cycle, which is one of the most common thermodynamic cycles that can be found in automobile engines. One of the key parameters of such engines is the change in volumes between the top dead center (TDC) to bottom dead center (BDC). The ratio of these volumes (V1 / V2) is known as the compression ratio. Also, the cut-off ratio is V3/V2, which is the ratio of volumes at the end and start of the combustion phase.
In this example, let us assume the Diesel cycle with a compression ratio of CR = 20 : 1 and cut-off ratio α = 2. The air is at 100 kPa = 1 bar, 20 °C (293 K), and the chamber volume is 500 cm³ before the compression stroke.
- Specific heat capacity at a constant air pressure at atmospheric pressure and room temperature: cp = 1.01 kJ/kgK.
- Specific heat capacity at constant air volume at atmospheric pressure and room temperature: cv = 0.718 kJ/kgK.
- κ = cp/cv = 1.4
Calculate:
- the mass of intake air
- the temperature T2
- the pressure p2
- the temperature T3
- the amount of heat added by burning of fuel-air mixture
- the thermal efficiency of this cycle
- the MEP
Solution:
1)
At the beginning of calculations, we must determine the amount of gas in the cylinder before the compression stroke. Using the ideal gas law, we can find the mass:
pV = mRspecificT
where:
- p is the absolute pressure of the gas
- m is the mass of the substance
- T is the absolute temperature
- V is the volume
- Rspecific is the specific gas constant, equal to the universal gas constant divided by the gas or mixture’s molar mass (M). For dry air Rspecific = 287.1 J.kg-1.K-1.
Therefore
m = p1V1/RspecificT1 = (100000 × 500×10-6 )/(287.1 × 293) = 5.95×10-4 kg
2)
In this problem all volumes are known:
- V1 = V4 = Vmax = 500×10-6 m3 (0.5l)
- V2 = Vmin = Vmax / CR = 25 ×10-6 m3
Note that (Vmax – Vmin) x number of cylinders = total engine displacement
Since the process is adiabatic, we can use the following p, V, T relation for adiabatic processes:
thus
T2 = T1 . CRκ – 1 = 293 . 200.4 = 971 K
3)
Again, we can use the ideal gas law to find the pressure at the end of the compression stroke as:
p2 = mRspecificT2 / V2 = 5.95×10-4 x 287.1 x 971 / 25 ×10-6 = 6635000 Pa = 66.35 bar
4)
Since process 2 → 3 occurs at constant pressure, the ideal gas equation of state gives
T3 = (V3/V2) x T2 = 1942 K
To calculate the amount of heat added by burning of fuel-air mixture, Qadd, we have to use the first law of thermodynamics for the isobaric process, which states:
Qadd = mcp (T3 – T2) = 5.95×10-4 x 1010 x 971 = 583.5 J
5)
Thermal efficiency for this Diesel cycle:
As was derived in the previous section, the thermal efficiency of the Diesel cycle is a function of the compression ratio, the cut-off ratio, and κ:
- ηDiesel is the maximum thermal efficiency of a Diesel cycle
- α is the cut-off ratio V3/V2 (i.e., the ratio of volumes at the end and start of the combustion phase)
- CR is the compression ratio
- κ = cp/cv = 1.4
For this example:
ηDiesel = 0.6467 = 64.7%
6)
The MEP was defined as:
In this equation, the displacement volume is equal to Vmax – Vmin. The network for one cycle can be calculated using the heat added and the thermal efficiency:
Wnet = Qadd . ηOtto = 583.5 x 0.6467 = 377.3 J
MEP = 377.3 / (500×10-6 – 25 ×10-6) = 794.3 kPa = 7.943 bar