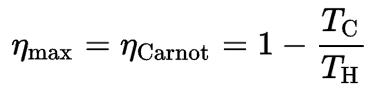
The Ericsson cycle is named after Swedish-American inventor John Ericsson, who designed and built many unique heat engines based on various thermodynamic cycles. He is credited with inventing two unique heat engine cycles and developing practical engines based on these cycles.
His first thermodynamic cycle, “the first Ericsson cycle,” is now called the “Brayton cycle“. It is the closed Brayton cycle, which is commonly applied to modern closed cycle gas turbine engines.
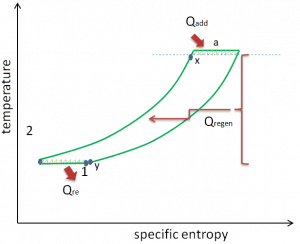
The second Ericsson cycle is what is now called the Ericsson cycle. The second Ericsson cycle is similar to the Brayton cycle but uses external heat and incorporates the multiple uses of an inter-cooling and reheat. It is like a Brayton cycle with an infinite number of reheat and intercooler stages in the cycle. Compared to the Brayton cycle, which uses adiabatic compression and expansion, an ideal Ericsson cycle consists of isothermal compression and expansion processes, combined with isobaric heat regeneration between them. Applying inter-cooling, heat regeneration, and sequential combustion significantly increase the thermal efficiency of a turbine. In fact, the thermal efficiency of the ideal Ericsson cycle equals the Carnot efficiency.
It is assumed (in an ideal case) that each intercooler returns the working fluid to the ambient temperature T1, and each reheater reheats the working fluid to the temperature T3. The regenerator is 100% efficient and allows the heat input for process 2 → 3 to be obtained from the heat rejected in process 4 → 1. Since there is no need for heat transfer (Qadd) in process 2 → 3, all the heat added externally would occur in the reheaters. All the heat rejected to the surroundings would take place in the intercoolers. As can be seen from the picture, in this case, all the heat added would occur when the working fluid is at its highest temperature, T3, and all the heat rejected would take place when the working fluid is at its lowest temperature, T1. Since irreversibilities are presumed absent, and all the heat is supplied and rejected isothermally, the thermal efficiency of an ideal Ericsson cycle can be calculated from these temperatures:
where:
- ηCarnot is the efficiency of the Carnot cycle, i.e., it is the ratio = W/QH of the work done by the engine to the heat energy entering the system from the hot reservoir.
- TC is the absolute temperature (Kelvins) of the cold reservoir,
- TH is the absolute temperature (Kelvins) of the hot reservoir.
Although the thermodynamic processes of the Ericsson cycle differ from those of the Carnot cycle, both cycles have the same value of thermal efficiency when operating between the temperatures TH and TC.