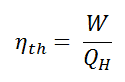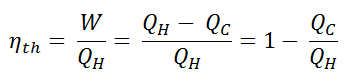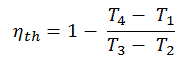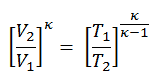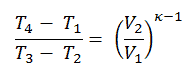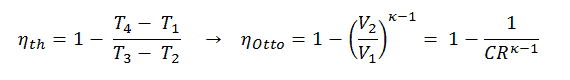Compression Ratio and Thermal Efficiency

Compression Ratio – Otto Engine

The compression ratio, CR, is defined as the ratio of the volume at the bottom dead center and the volume at the top dead center. It is a key characteristic of many internal combustion engines. In the following section, it will be shown that the compression ratio determines the thermal efficiency of the used thermodynamic cycle of the combustion engine. It is desired to have a high compression ratio because it allows an engine to reach higher thermal efficiency.

For example, let assume an Otto cycle with compression ratio of CR = 10 : 1. The volume of the chamber is 500 cm³ = 500×10^-6 m³ (0.5l) prior to the compression stroke. For this engine all required volumes are known:

V₁ = V₄ = V_max = 500×10^-6 m³ (0.5l)
V₂ = V₃ = V_min = V_max / CR = 55.56 ×10^-6 m³

Note that (V_max – V_min) x number of cylinders = total engine displacement.

Thermal Efficiency for Otto Cycle

In general, the thermal efficiency, η_th, of any heat engine is defined as the ratio of the work it does, W, to the heat input at the high temperature, Q_H.

The thermal efficiency, η_th, represents the fraction of heat, Q_H, converted to work. Since energy is conserved according to the first law of thermodynamics and energy cannot be converted to work completely, the heat input, Q_H, must equal the work done, W, plus the heat that must be dissipated as waste heat Q_C into the environment. Therefore we can rewrite the formula for thermal efficiency as:

The heat absorbed occurs during combustion of fuel-air mixture, when the spark occurs, roughly at constant volume. Since during an isochoric process there is no work done by or on the system, the first law of thermodynamics dictates ∆U = ∆Q. Therefore, the heat added and rejected is given by:

Q_add = mc_v (T₃ – T₂)

Q_out = mc_v (T₄ – T₁)

Substituting these expressions for the heat added and rejected in the expression for thermal efficiency yields:

We can simplify the above expression using the fact that the processes 1 → 2 and from 3 → 4 are adiabatic, and for an adiabatic process, the following p,V,T formula is valid:

It can be derived that:

In this equation, the ratio V₁/V₂ is known as the compression ratio, CR. When we rewrite the expression for thermal efficiency using the compression ratio, we conclude the air-standard Otto cycle thermal efficiency is a function of compression ratio and κ = c_p/c_v.

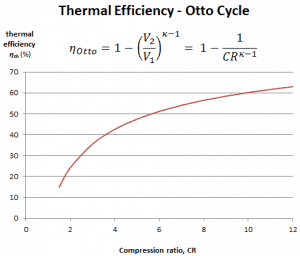
thermal efficiency - Otto Cycle - Engine — Thermal efficiency for Otto cycle – κ = 1.4

It is a very useful conclusion because it is desirable to achieve a high compression ratio to extract more mechanical energy from a given mass of the air-fuel mixture. A higher compression ratio permits the same combustion temperature to be reached with less fuel while giving a longer expansion cycle. This creates more mechanical power output and lowers the exhaust temperature. Lowering the exhaust temperature causes the lowering of the energy rejected to the atmosphere. This relationship is shown in the figure for κ = 1.4, representing ambient air.

References:

Nuclear and Reactor Physics:

J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
Kenneth S. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN: 978-0471805533
G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See above:

Otto Cycle