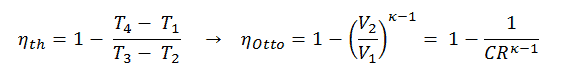The compression ratio, CR, is defined as the ratio of the volume at the bottom dead center and the volume at the top dead center. It is a key characteristic of many internal combustion engines. In the following section, it will be shown that the compression ratio determines the thermal efficiency of the used thermodynamic cycle of the combustion engine. It is desired to have a high compression ratio because it allows an engine to reach higher thermal efficiency.
For example, let assume an Otto cycle with compression ratio of CR = 10 : 1. The volume of the chamber is 500 cm³ = 500×10-6 m3 (0.5l) prior to the compression stroke. For this engine all required volumes are known:
- V1 = V4 = Vmax = 500×10-6 m3 (0.5l)
- V2 = V3 = Vmin = Vmax / CR = 55.56 ×10-6 m3
Note that (Vmax – Vmin) x number of cylinders = total engine displacement.
Examples of Compression Ratios – Gasoline vs. Diesel
- The compression ratio in a gasoline-powered engine will usually not be much higher than 10:1 due to potential engine knocking (autoignition) and not lower than 6:1.
- A turbocharged Subaru Impreza WRX has a compression ratio of 8.0:1. In general, turbocharged or supercharged engines already have compressed air at the air intake. Therefore they are usually built with a lower compression ratio.
- A stock Honda S2000 engine (F22C1) has a compression ratio of 11.1:1.
- Some atmospheric sportscar engines can have a compression ratio up to 12.5 : 1 (e.g.,, Ferrari 458 Italia).
- In 2012, Mazda released new petrol engines under the brand name SkyActiv with a 14:1 compression ratio. Residual gas is reduced by using 4-2-1 engine exhaust systems, implementing a piston cavity, and optimizing fuel injection to reduce the risk of engine knocking.
- The Diesel engines have a compression ratio that normally exceeds 14:1, and ratios over 22:1 are also common.
Thermal Efficiency for Otto Cycle
The air-standard Otto cycle thermal efficiency is a function of compression ratio and κ = cp/cv.
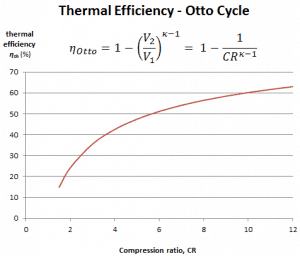
It is a very useful conclusion because it is desirable to achieve a high compression ratio to extract more mechanical energy from a given mass of the air-fuel mixture. A higher compression ratio permits the same combustion temperature to be reached with less fuel while giving a longer expansion cycle. This creates more mechanical power output and lowers the exhaust temperature. Lowering the exhaust temperature causes the lowering of the energy rejected to the atmosphere. This relationship is shown in the figure for κ = 1.4, representing ambient air.
Autoignition – Limit for Compression Ratio
In ordinary gasoline engines, the compression ratio has its limits. The compression ratio in a gasoline-powered engine will usually not be much higher than 10:1 due to potential engine knocking (autoignition) and not lower than 6:1. However, higher compression ratios will make gasoline engines subject to engine knocking, caused by the autoignition of an unburned mixture, if lower octane-rated fuel is used. The unburned mixture may auto-ignite by detonating from pressure and heat alone rather than igniting the spark plug at exactly the right time. The engine knocking can be reduced by using high-octane fuel, which increases the gasoline’s resistance to autoignition. The higher the octane number, the more compression the fuel can withstand before detonating (igniting). Since the temperature attained by the fuel-air mixture during the compression increases as the compression ratio increases, the likelihood of autoignition increases with the compression ratio. The autoignition can reduce efficiency or damage the engine if knock sensors are not present to modify the ignition timing.
Higher compression ratios can be achieved in diesel engines (also called compression-ignition engines) because they do not compress the fuel but rather compress only air and then inject fuel into the air, which was heated by compression. Compression ratios in the range of 12 to 20 are typical for diesel engines. The greater expansion in diesel engines means they reject less heat in their cooler exhaust. The higher compression ratio (greater expansion) and the higher peak temperature causes that diesel engines reach higher thermal efficiency.