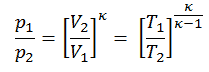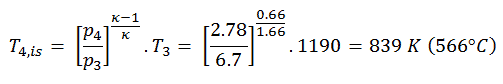Example of Isentropic Process

Example: Isentropic Expansion in Gas Turbine

P-V diagram - isentropic process — P-V diagram of an isentropic expansion of helium (3 → 4) in a gas turbine.

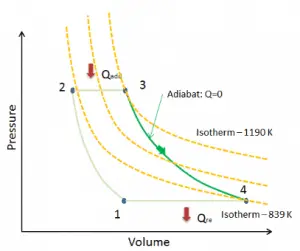
Assume an isentropic expansion of helium (3 → 4) in a gas turbine. Since helium behaves almost as an ideal gas, use the ideal gas law to calculate the outlet temperature of the gas (T_4,is). In these turbines, the high-pressure stage receives gas (point 3 at the figure; p₃= 6.7 MPa; T₃ = 1190 K (917°C)) from a heat exchanger and exhaust it to another heat exchanger, where the outlet pressure is p₄ = 2.78 MPa (point 4).

Solution:

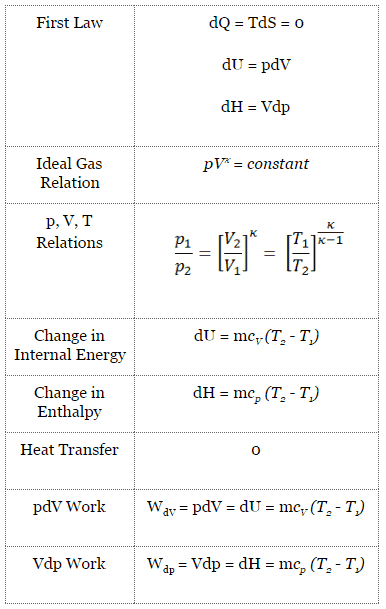
The outlet temperature of the gas, T_4,is, can be calculated using p, V, T Relation for isentropic process (reversible adiabatic process):

In this equation the factor for helium is equal to κ=c_p/c_v=1.66. From the previous equation follows that the outlet temperature of the gas, T_4,is, is:

Isentropic Process - characteristics — Table of main characteristics

Example: Isentropic Expansion in Gas Turbine

first law - example - brayton cycle — The ideal Brayton cycle consists of four thermodynamic processes. Two isentropic processes and two isobaric processes.

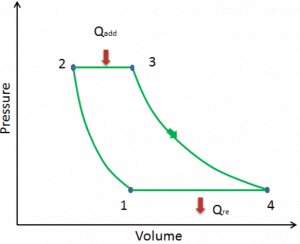
Let assume the ideal Brayton cycle that describes the workings of a constant pressure heat engine. Modern gas turbine engines and airbreathing jet engines also follow the Brayton cycle.

The ideal Brayton cycle consists of four thermodynamic processes. Two isentropic processes and two isobaric processes.

Isentropic compression – ambient air is drawn into the compressor, pressurized (1 → 2). The work required for the compressor is given by W_C = H₂ – H₁.
Isobaric heat addition – the compressed air then runs through a combustion chamber, burning fuel, and air or another medium is heated (2 → 3). It is a constant-pressure process since the chamber is open to flow in and out. The net heat added is given by Q_add = H₃– H₂
Isentropic expansion – the heated, pressurized air then expands on a turbine, gives up its energy. The work done by the turbine is given by W_T = H₄ – H₃
Isobaric heat rejection – the residual heat must be rejected to close the cycle. The net heat rejected is given by Q_re = H₄– H₁

As can be seen, we can describe and calculate (e.g.,, thermal efficiency) such cycles (similarly for Rankine cycle) using enthalpies.

References:

Nuclear and Reactor Physics:

J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
Kenneth S. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN: 978-0471805533
G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2.
E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See above:

Isentropic Process