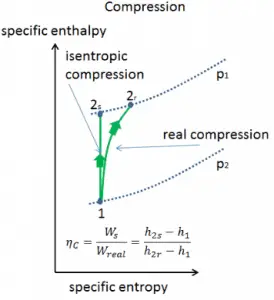
In previous chapters, we assumed that the gas expansion is isentropic, and therefore we used T4,is as the gas´s temperature outlet. These assumptions are only applicable with ideal cycles.
Most steady-flow devices (turbines, compressors, nozzles) operate under adiabatic conditions, but they are not truly isentropic but are rather idealized as isentropic for calculation purposes. We define parameters ηT, ηC, ηN, as a ratio of real work done by a device to work by a device when operated under isentropic conditions (in the case of the turbine). This ratio is known as the Isentropic Turbine/Compressor/Nozzle Efficiency.
These parameters describe how efficiently a turbine, compressor, or nozzle approximates a corresponding isentropic device. This parameter reduces the overall efficiency and work output. For turbines, the value of ηT is typically 0.7 to 0.9 (70–90%).
Example: Isentropic Turbine Efficiency
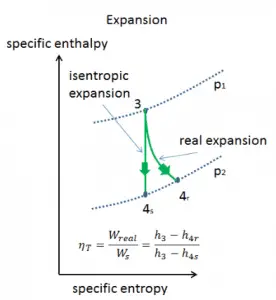
Assume an isentropic expansion of helium (3 → 4) in a gas turbine. In these turbines, the high-pressure stage receives gas (point 3 at the figure; p3 = 6.7 MPa; T3 = 1190 K (917°C)) from a heat exchanger and exhaust it to another heat exchanger, where the outlet pressure is p4 = 2.78 MPa (point 4). The temperature (for the isentropic process) of the gas at the exit of the turbine is T4s = 839 K (566°C).
Calculate the work done by this turbine and calculate the real temperature at the exit of the turbine when the isentropic turbine efficiency is ηT = 0.91 (91%).
Solution:
From the first law of thermodynamics, the work done by the turbine in an isentropic process can be calculated from:
WT = h3 – h4s → WTs = cp (T3 – T4s)
From Ideal Gas Law we know, that the molar specific heat of a monatomic ideal gas is:
Cv = 3/2R = 12.5 J/mol K and Cp = Cv + R = 5/2R = 20.8 J/mol K
We transfer the specific heat capacities into units of J/kg K via:
cp = Cp . 1/M (molar weight of helium) = 20.8 x 4.10-3 = 5200 J/kg K
The work done by gas turbine in isentropic process is then:
WT,s = cp (T3 – T4s) = 5200 x (1190 – 839) = 1.825 MJ/kg
The real work done by gas turbine in adiabatic process is then:
WT,real = cp (T3 – T4s) . ηT = 5200 x (1190 – 839) x 0.91 = 1.661 MJ/kg