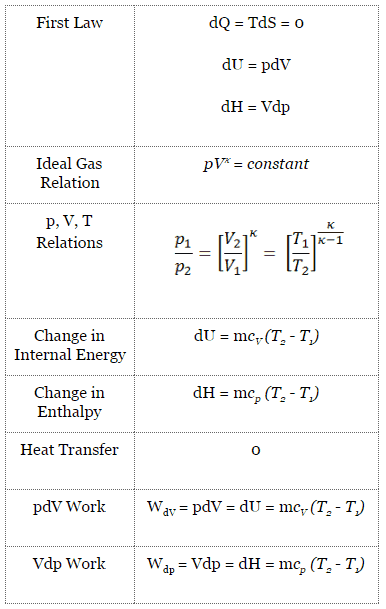
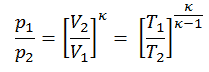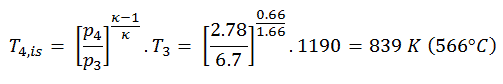An isentropic process is a thermodynamic process in which the entropy of the fluid or gas remains constant. It means the isentropic process is a special case of an adiabatic process in which there is no transfer of heat or matter. It is a reversible adiabatic process.
Expansion and Compression of Ideal Gases
See also: What is an Ideal Gas
In an ideal gas, molecules have no volume and do not interact. According to the ideal gas law, pressure varies linearly with temperature and quantity and inversely with volume.
pV = nRT
where:
- p is the absolute pressure of the gas
- n is the amount of substance
- T is the absolute temperature
- V is the volume
- R is the ideal, or universal, gas constant, equal to the product of the Boltzmann constant and the Avogadro constant,
In this equation, the symbol R is the universal gas constant with the same value for all gases—namely, R = 8.31 J/mol K.
The isentropic process (a special case of the adiabatic process) can be expressed with the ideal gas law as:
pVκ = constant
or
p1V1κ = p2V2κ
in which κ = cp/cv is the ratio of the specific heats (or heat capacities) for the gas. One for constant pressure (cp) and one for constant volume (cv). Note that this ratio κ = cp/cv is a factor in determining the speed of sound in gas and other adiabatic processes.
Other p, V, T Relation
On a p-V diagram, the process occurs along a line (called an adiabat) that has the equation p = constant / Vκ. For an ideal gas and a polytropic process, the case n = κ corresponds to an isentropic process.
See also: First Law of Thermodynamics
See also: Ideal Gas Law
See also: What is Enthalpy
Example: Isentropic Expansion in Gas Turbine
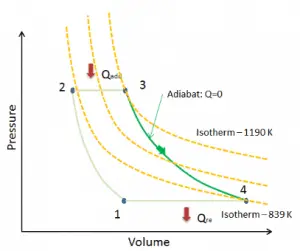
Assume an isentropic expansion of helium (3 → 4) in a gas turbine. Since helium behaves almost as an ideal gas, use the ideal gas law to calculate the outlet temperature of the gas (T4, is). In these turbines, the high-pressure stage receives gas (point 3 at the figure; p3 = 6.7 MPa; T3 = 1190 K (917°C)) from a heat exchanger and exhaust it to another heat exchanger, where the outlet pressure is p4 = 2.78 MPa (point 4).
Solution:
The outlet temperature of the gas, T4,is, can be calculated using p, V, T Relation for isentropic process (reversible adiabatic process):
In this equation the factor for helium is equal to κ=cp/cv=1.66. From the previous equation follows that the outlet temperature of the gas, T4,is, is:
Example: Isentropic Expansion in Gas Turbine
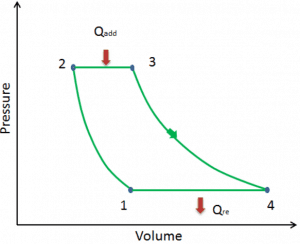
Let assume the ideal Brayton cycle that describes the workings of a constant pressure heat engine. Modern gas turbine engines and airbreathing jet engines also follow the Brayton cycle.
The ideal Brayton cycle consists of four thermodynamic processes. Two isentropic processes and two isobaric processes.
- Isentropic compression – ambient air is drawn into the compressor, pressurized (1 → 2). The work required for the compressor is given by WC = H2 – H1.
- Isobaric heat addition – the compressed air then runs through a combustion chamber, burning fuel, and air or another medium is heated (2 → 3). It is a constant-pressure process since the chamber is open to flow in and out. The net heat added is given by Qadd = H3 – H2
- Isentropic expansion – the heated, pressurized air then expands on the turbine, gives up its energy. The work done by the turbine is given by WT = H4 – H3
- Isobaric heat rejection – the residual heat must be rejected to close the cycle. The net heat rejected is given by Qre = H4 – H1
As can be seen, we can describe and calculate (e.g.,, thermal efficiency) such cycles (similarly for Rankine cycle) using enthalpies.
See also: Thermal Efficiency of Brayton Cycle