Facebook Instagram Youtube Twitter

Example of Isobaric Process – Isobaric Heat Addition

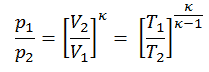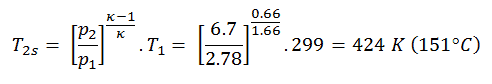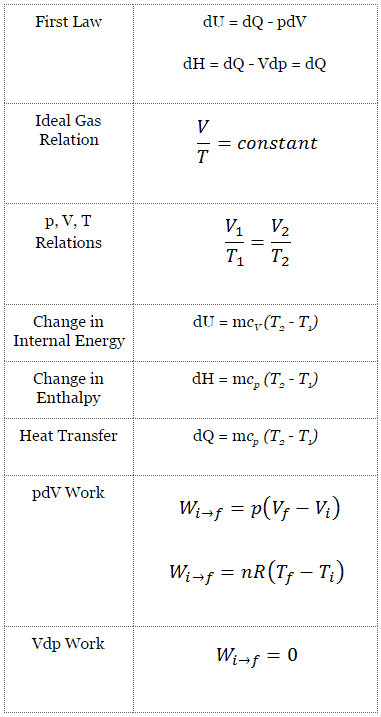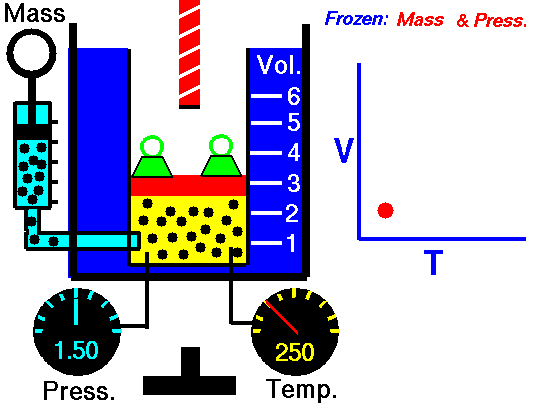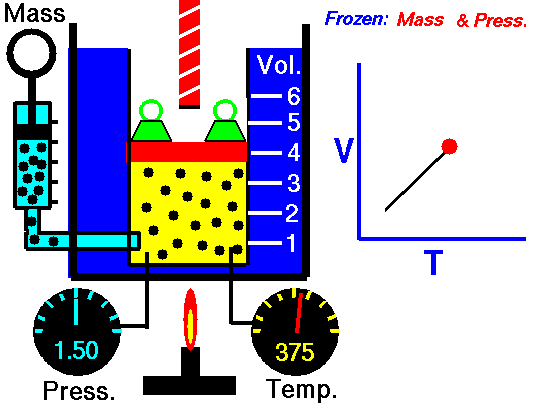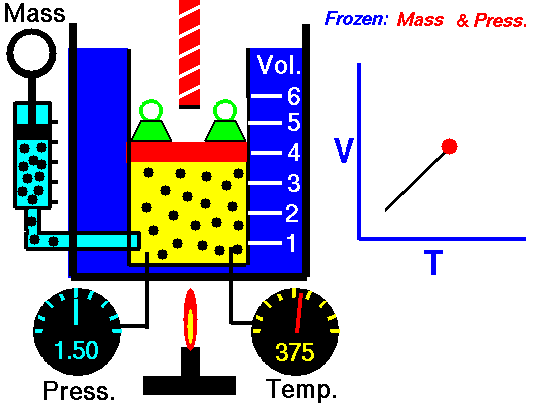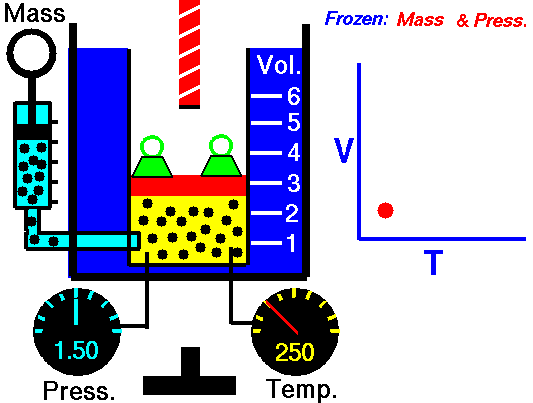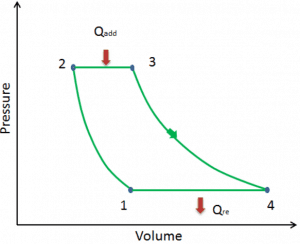
first law - example - brayton cycle
The ideal Brayton cycle consists of four thermodynamic processes. Two isentropic processes and two isobaric processes.

Let assume the ideal Brayton cycle that describes the workings of a constant pressure heat engine. Modern gas turbine engines and airbreathing jet engines also follow the Brayton cycle.

The ideal Brayton cycle consists of four thermodynamic processes. Two isentropic processes and two isobaric processes.

  1. Isentropic compression – ambient air is drawn into the compressor, pressurized (1 → 2). The work required for the compressor is given by WC = H2 – H1.
  2. Isobaric heat addition – the compressed air then runs through a combustion chamber, burning fuel, and air or another medium is heated (2 → 3). It is a constant-pressure process since the chamber is open to flow in and out. The net heat added is given by Qadd = H3 – H2
  3. Isentropic expansion – the heated, pressurized air then expands on a turbine, gives up its energy. The work done by the turbine is given by WT = H4 – H3
  4. Isobaric heat rejection – the residual heat must be rejected to close the cycle. The net heat rejected is given by Qre = H4 – H1

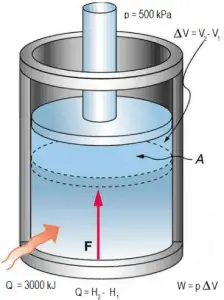
Assume an isobaric heat addition (2 → 3) in a heat exchanger. In typical gas turbines, the high-pressure stage receives gas (point 3 at the figure; p3 = 6.7 MPa; T3 = 1190 K (917°C)) from a heat exchanger. Moreover, we know that the compressor receives gas (point 1 at the figure; p1 = 2.78 MPa; T1 = 299 K (26°C)), and we know that the isentropic efficiency of the compressor is ηK = 0.87 (87%).

Calculate the heat added by the heat exchanger (between 2 → 3).

Solution:

From the first law of thermodynamics, the net heat added is given by Qadd = H3 – H2 or Qadd = Cp.(T3-T2s), but we do not know the temperature (T2s) at the outlet of the compressor. We will solve this problem in intensive variables. We have to rewrite the previous equation (to include ηK) using the term (+h1 – h1) to:

Qadd = h3 – h2 = h3 – h1 – (h2s – h1)/ηK  

Qadd = cp(T3-T1) – (cp(T2s-T1)/ηK)

Then we will calculate the temperature, T2s, using p, V, T Relation for the adiabatic process between (1 → 2).

p,V,T relation - isentropic process

In this equation, the factor for helium is equal to =cp/cv=1.66. The previous equation follows that the compressor outlet temperature, T2s, is:

isobaric process - example

From Ideal Gas Law we know, that the molar specific heat of a monatomic ideal gas is:

Cv = 3/2R = 12.5 J/mol K and Cp = Cv + R = 5/2R = 20.8 J/mol K

We transfer the specific heat capacities into units of J/kg K via:

cp = Cp . 1/M (molar weight of helium) = 20.8 x 4.10-3 = 5200 J/kg K

Using this temperature and the isentropic compressor efficiency we can calculate the heat added by the heat exchanger:

Qadd = cp(T3-T1) – (cp(T2s-T1)/ηK) = 5200.(1190 – 299) – 5200.(424-299)/0.87 = 4.633 MJ/kg – 0.747 MJ/kg = 3.886 MJ/kg

Isobaric process - main characteristics
Isobaric process – main characteristics
Charles's Law is one of the gas laws.
The volume is directly proportional to the Kelvin temperature for a fixed mass of gas at constant pressure. Source: grc.nasa.gov NASA copyright policy states that “NASA material is not protected by copyright unless noted”.
 
Example: Frictionless Piston – Heat – Enthalpy
Enthalpy - Example - A frictionless piston
Calculate the final temperature if 3000 kJ of heat is added.

A frictionless piston is used to provide a constant pressure of 500 kPa in a cylinder containing steam (superheated steam) of a volume of 2 m3  at 500 K. Calculate the final temperature if 3000 kJ of heat is added.

Solution:

Using steam tables we know, that the specific enthalpy of such steam (500 kPa; 500 K) is about 2912 kJ/kg. Since the steam has a density of 2.2 kg/m3, we know about 4.4 kg of steam in the piston at an enthalpy of 2912 kJ/kg x 4.4 kg = 12812 kJ.

When we use simply Q = H2 − H1, then the resulting enthalpy of steam will be:

H2 = H1 + Q = 15812 kJ

From steam tables, such superheated steam (15812/4.4 = 3593 kJ/kg) will have a temperature of 828 K (555°C). Since at this enthalpy, the steam has a density of 1.31 kg/m3, it is obvious that it has expanded by about 2.2/1.31 = 1.67 (+67%). Therefore the resulting volume is 2 m3 x 1.67 = 3.34 m3 and ∆V = 3.34 m3 – 2 m3 = 1.34 m3.

The p∆V part of enthalpy, i.e., the work done, is:

W = p∆V = 500 000 Pa x 1.34 m3 = 670 kJ

 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. Kenneth S. Krane. Introductory Nuclear Physics, 3rd Edition, Wiley, 1987, ISBN: 978-0471805533
  7. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  8. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  9. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2. 
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See above:

Isobaric Process