Temperature Scales
 When using a thermometer, we need to mark a scale on the tube wall with numbers on it. We have to define a temperature scale. A temperature scale is a way to measure temperature relative to a starting point (0 or zero) and a unit of measurement.
When using a thermometer, we need to mark a scale on the tube wall with numbers on it. We have to define a temperature scale. A temperature scale is a way to measure temperature relative to a starting point (0 or zero) and a unit of measurement.
These numbers are arbitrary, and historically many different schemes have been used. For example, this was done by defining some physical occurrences at given temperatures—such as the freezing and boiling points of water — and defining them as 0 and 100, respectively.
There are several scales and units exist for measuring temperature. The most common are:
Fahrenheit Scale – Fahrenheit Temperature
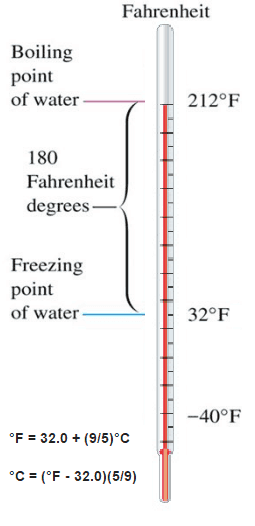
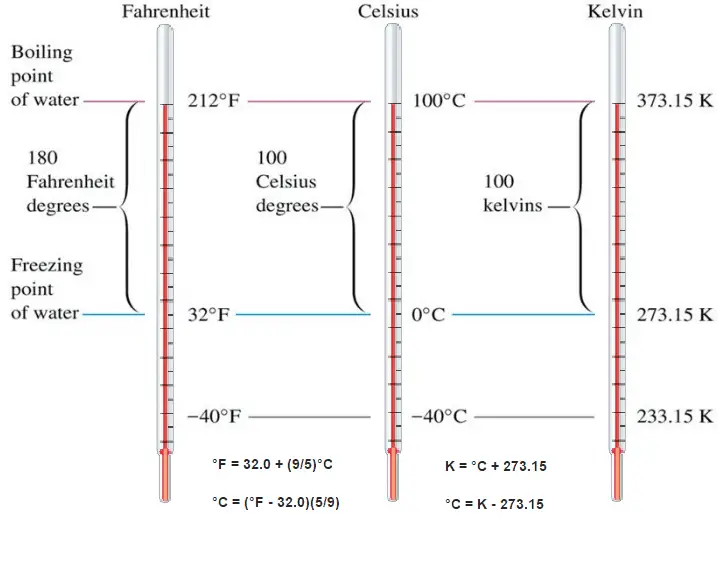
The Celsius scale and the Fahrenheit scale are based on a specification of the number of increments between the freezing point and boiling point of water at standard atmospheric pressure. The Celsius scale has 100 units between these points, and the Fahrenheit scale has 180 units, where each unit represents 1°C or 1 °F, respectively. The zero points on the scales are arbitrary.
Fahrenheit scale is based on two points:
- The lower defining point, 0 °F, was established as the temperature of a solution of brine made from equal parts of ice and salt.
- The upper defining point, 96 °F, was established as the average human body temperature (96 °F, about 2.6 °F less than the modern value due to a later redefinition of the scale)
The difference in height between the two points would then be marked off in 180 divisions, with each division representing 1 °F. Today, the scale is usually defined by two fixed points: the temperature at which water freezes into ice is 32 °F, and the boiling point of water is 212 °F.
Temperature Conversion – Fahrenheit – Celsius
To convert from a Fahrenheit temperature to a Celsius temperature, we have to subtract 32 degrees from the Fahrenheit reading to get to the zero point on the Celsius scale and then adjust for the different size degrees. The ratio of the size of the degrees is 5/9 so that the relationship between the scales is represented by the following equations:
°F = 32.0 + (9/5)°C
°C = (°F – 32.0)(5/9)