When using a thermometer, we need to mark a scale on the tube wall with numbers on it. We have to define a temperature scale. A temperature scale is a way to measure temperature relative to a starting point (0 or zero) and a unit of measurement.
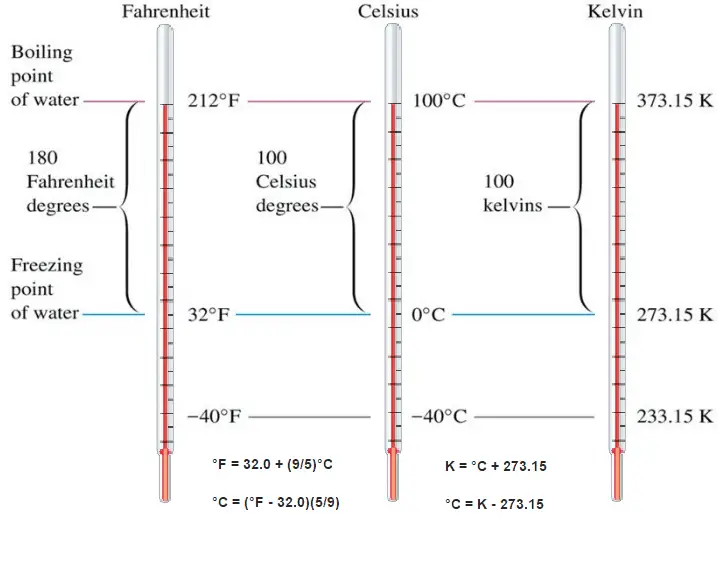
These numbers are arbitrary, and historically many different schemes have been used. For example, this was done by defining some physical occurrences at given temperatures—such as the freezing and boiling points of water — and defining them as 0 and 100, respectively.
There are several scales and units exist for measuring temperature. The most common are:
- Celsius (denoted °C),
- Fahrenheit (denoted °F),
- Kelvin (denoted K; especially in science).
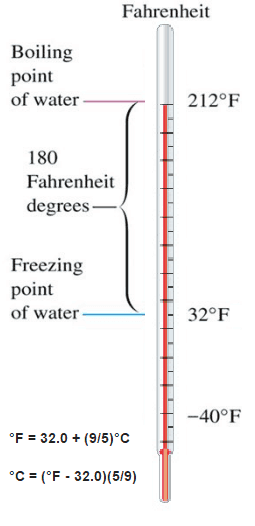
The Celsius scale and the Fahrenheit scale are based on a specification of the number of increments between the freezing point and boiling point of water at standard atmospheric pressure. The Celsius scale has 100 units between these points, and the Fahrenheit scale has 180 units, where each unit represents 1°C or 1 °F, respectively. The zero points on the scales are arbitrary.
Fahrenheit scale is based on two points:
- The lower defining point, 0 °F, was established as the temperature of a solution of brine made from equal parts of ice and salt.
- The upper defining point, 96 °F, was established as the average human body temperature (96 °F, about 2.6 °F less than the modern value due to a later redefinition of the scale)
The difference in height between the two points would then be marked off in 180 divisions, with each division representing 1 °F. Today, the scale is usually defined by two fixed points: the temperature at which water freezes into ice is 32 °F, and the boiling point of water is 212 °F.
Temperature Conversion – Fahrenheit – Celsius
To convert from a Fahrenheit temperature to a Celsius temperature, we have to subtract 32 degrees from the Fahrenheit reading to get to the zero point on the Celsius scale and then adjust for the different size degrees. The ratio of the size of the degrees is 5/9 so that the relationship between the scales is represented by the following equations:
°F = 32.0 + (9/5)°C
°C = (°F – 32.0)(5/9)
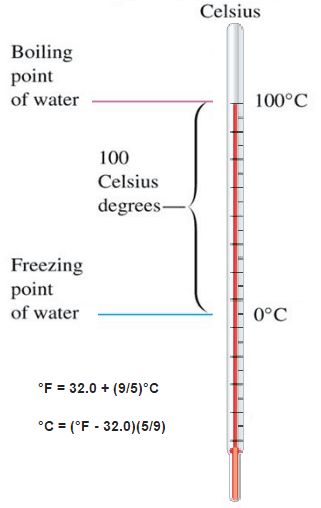
About 20 years after Fahrenheit proposed its temperature scale for thermometer, Swedish professor Anders Celsius defined a better scale for measuring temperature. He proposed using the boiling point of water as 100° C and the freezing point of water as 0° C. Water was chosen as the reference material because it was always available in most laboratories worldwide.
Celsius temperature scale is also called the centigrade temperature scale because of the 100-degree interval between the defined points. The Celsius temperature for a state colder than freezing water is a negative number. The Celsius scale is used, both in everyday life and in science and industry, almost everywhere globally.
Absolute zero, the lowest temperature possible, is defined as being precisely 0 K and −273.15 °C. The temperature of the triple point of water is defined as precisely 273.16 K and 0.01 °C. This definition fixes the magnitude of both the degree Celsius and the kelvin as precisely 1 part in 273.16 of the difference between absolute zero and the triple point of water.
It must be added, by international agreement the unit “degree Celsius” and the Celsius scale are currently defined by two different points: absolute zero and the triple point of water (instead of boiling and freezing points). This definition also precisely relates the Celsius scale to the Kelvin scale, which defines the SI base unit of thermodynamic temperature.
Temperature Conversion – Fahrenheit – Celsius
To convert from a Fahrenheit temperature to a Celsius temperature, we have to subtract 32 degrees from the Fahrenheit reading to get to the zero point on the Celsius scale and then adjust for the different size degrees. The ratio of the size of the degrees is 5/9 so that the relationship between the scales is represented by the following equations:
°F = 32.0 + (9/5)°C
°C = (°F – 32.0)(5/9)
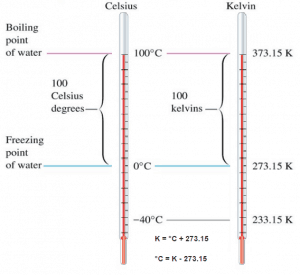
Kelvin temperature scale is the base unit of thermodynamic temperature measurement in the International System (SI) of measurement. The Kelvin scale was determined based on the Celsius scale but with a starting point at absolute zero. Temperatures in the Kelvin scale are 273 degrees less than in the Celsius scale. The kelvin is defined as the fraction 1⁄273.16 of the thermodynamic temperature of the triple point of water. By international agreement, the triple point of water has been assigned a value of 273.16 K (0.01 °C; 32.02 °F) and partial vapor pressure of 611.66 pascals (6.1166 mbar; 0.0060366 atm). In other words, it is defined such that the triple point of water is exactly 273.16 K.
Note that the unit on the absolute scale is Kelvins, not degrees Kelvin. It was named in honor of Lord Kelvin, who had a great deal to do with temperature measurement and thermodynamics development.
The absolute temperature scale that corresponds to the Celsius scale is called the Kelvin (K) scale, and the absolute scale that corresponds to the Fahrenheit scale is called the Rankine (R) scale. The zero points on both absolute scales represent the same physical state. The relationships between the absolute and relative temperature scales are shown in the following equations.
Kelvin – Celsius
K = °C + 273.15
°C = K – 273.15
Rankine – Fahrenheit
R = °F + 460
°F = R – 460
Absolute Zero
Such a scale has as its zero point. The coldest theoretical temperature is called absolute zero, at which the thermal motion of atoms and molecules reaches its minimum. This is a state at which the enthalpy and entropy of a cooled ideal gas reach its minimum value, taken as 0. Classically, this would be a state of motionlessness, but quantum uncertainty dictates that the particles still possess finite zero-point energy. Absolute zero is denoted as 0 K on the Kelvin scale, −273.15 °C on the Celsius scale, and −459.67 °F on the Fahrenheit scale.
Absolute Zero and Third Law of Thermodynamics
Third law of thermodynamics states:
The entropy of a system approaches a constant value as the temperature approaches absolute zero.
Based on empirical evidence, this law states that the entropy of a pure crystalline substance is zero at the absolute zero of temperature, 0 K and that it is impossible by means of any process, no matter how idealized, to reduce the temperature of a system to absolute zero in a finite number of steps. This allows us to define a zero point for the thermal energy of a body.
