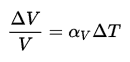Facebook Instagram Youtube Twitter

What is Volume – Physics

Volume is a basic physical quantity. Volume is a derived quantity, and it expresses the three-dimensional extent of an object. Volume is often quantified numerically using the SI-derived unit, the cubic meter.

For example, the volume inside a sphere (that is, the volume of a ball) is derived from being V = 4/3πr3, where r is the sphere’s radius. As another example, the volume of a cube is equal to side times side. Since each side of a square is the same, it can simply be the length of one side cubed.

If a square has one side of 3 meters, the volume would be 3 meters times 3 meters times 3 meters, or 27 cubic meters.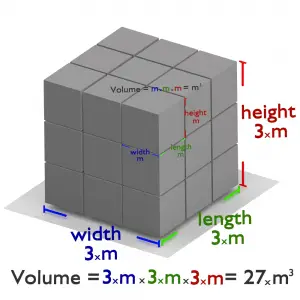what is volume - physics

Formulas for Calculation of Different Volumes
Volume formulas for some common three-dimensional objects:

formulas-for-volume-calculations-min

What is Specific Volume

Density - Gas - Liquid - Solid
Typical densities of various substances at atmospheric pressure.

Specific volume is an intensive variable, whereas volume is an extensive variable. The SI system’s standard unit for specific volumes is cubic meters per kilogram (m3/kg). The standard unit in the English system is cubic feet per pound-mass (ft3/lbm).

The density (ρ) of a substance is the reciprocal of its specific volume (ν).

ρ = m/V = 1/ρ

Density is defined as the mass per unit volume. It is also an intensive property, which is mathematically defined as mass divided by volume:

ρ = m/V

Materials with Lowest Specific Volume - Densest Materials on the Earth
Since nucleons (protons and neutrons) make up most of the mass of ordinary atoms, the density of normal matter tends to be limited by how closely we can pack these nucleons and depends on the internal atomic structure of a substance. The densest material found on earth is the metal osmium. Still, its density pales by comparison to the densities of exotic astronomical objects such as white dwarf stars and neutron stars.

List of densest materials:

  1. Osmium – 22.6 x 103 kg/m3
  2. Iridium – 22.4 x 103 kg/m3
  3. Platinum – 21.5 x 103 kg/m3
  4. Rhenium – 21.0 x 103 kg/m3
  5. Plutonium – 19.8 x 103 kg/m3
  6. Gold – 19.3 x 103 kg/m3
  7. Tungsten – 19.3 x 103 kg/m3
  8. Uranium – 18.8 x 103 kg/m3
  9. Tantalum – 16.6 x 103 kg/m3
  10. Mercury – 13.6 x 103 kg/m3
  11. Rhodium – 12.4 x 103 kg/m3
  12. Thorium – 11.7 x 103 kg/m3
  13. Lead – 11.3 x 103 kg/m3
  14. Silver – 10.5 x 103 kg/m3

It must be noted, plutonium is a manufactured isotope and is created from uranium in nuclear reactors. But scientists have found trace amounts of naturally-occurring plutonium.

If we include manufactured elements, the densest so far is Hassium. Hassium is a chemical element with the symbol Hs and atomic number 108.  It is a synthetic element (first synthesized at Hasse in Germany) and radioactive. The most stable known isotope, 269Hs, has a half-life of approximately 9.7 seconds. It has an estimated density of 40.7 x 103 kg/m3.  The density of Hassium results from its high atomic weight and the significant decrease in ionic radii of the elements in the lanthanide series, known as lanthanide and actinide contraction.

The density of Hassium is followed by Meitnerium (element 109, named after the physicist Lise Meitner), which has an estimated density of 37.4 x 103 kg/m3.

Changes in Specific Volume
In general, density and thus the specific volume can be changed by changing either the pressure or the temperature. Increasing the pressure always increases the density of a material. The effect of pressure on the densities of liquids and solids is very small. On the other hand, the density of gases is strongly affected by pressure. This is expressed by compressibility. Compressibility measures the relative volume change of a fluid or solid as a response to a pressure change.

The effect of temperature on the densities of liquids and solids is also very important. Most substances expand when heated and contract when cooled. However, the amount of expansion or contraction varies, depending on the material. This phenomenon is known as thermal expansion. The change in volume of a material that undergoes a temperature change is given by the following relation:

thermal-expansion

where ∆T is the temperature change, V is the original volume, ∆V is the volume change, and αV is the coefficient of volume expansion.

It must be noted and there are exceptions to this rule. For example, water differs from most liquids in that it becomes less dense as it freezes. It has a maximum density of 3.98 °C (1000 kg/m3), whereas the density of ice is 917 kg/m3. It differs by about 9% and therefore ice floats on liquid water

The volume of an Atom and Nucleus

Structure of Matter.
Structure of Matter.

The atom consists of a small but massive nucleus surrounded by a cloud of rapidly moving electrons. The nucleus is composed of protons and neutrons. Typical nuclear radii are of the order 10−14 m. Nuclear radii can be calculated according to the following formula assuming spherical shape:

r = r0 . A1/3

where r0 = 1.2 x 10-15 m = 1.2 fm

If we use this approximation, we, therefore, expect the volume of the nucleus to be of the order of 4/3πr3 or 7,23 ×10−45 m3 for hydrogen nuclei or 1721×10−45 m3 for 238U nuclei. These are nuclei volumes, and atomic nuclei (protons and neutrons) contain about 99.95% of the atom’s mass.

Is an atom an empty space?

atomic-nucleus-volume-min
A figurative depiction of the helium-4 atom with the electron cloud in shades of gray. Protons and neutrons are most likely found in the same space, at the central point. Source wikipedia.org License CC BY-SA 3.0

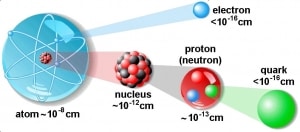
The volume of an atom is about 15 orders of magnitude larger than the volume of a nucleus. For uranium atom, the Van der Waals radius is about 186 pm = 1.86 ×10−10 m. The Van der Waals radius, rw, of an atom is the radius of an imaginary hard-sphere representing the distance of closest approach for another atom.  The uranium atom has a volume of about  26.9 ×10−30 m3,  assuming a spherical shape. But this “huge” space is occupied primarily by electrons because the nucleus occupies only about 1721×10−45 m3 of space. These electrons together weigh only a fraction (let say 0.05%) of the entire atom.

It may seem that the space and the matter are empty, but it is not. Due to the quantum nature of electrons, the electrons are not pointing particles, and they are smeared out over the whole atom. The classical description cannot be used to describe things on the atomic scale. On the atomic scale, physicists have found that quantum mechanics describes things very well on that scale. Particle locations in quantum mechanics are not at an exact position, and they are described by a probability density function. Therefore the space in an atom (between electrons and an atomic nucleus) is not empty. Still, it is filled by a probability density function of electrons (usually known as “electron cloud”).

The volume of Coolant in Reactor Coolant System

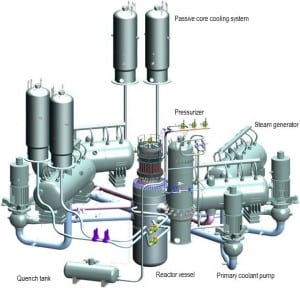
Nuclear reactor - WWER 1200
Nuclear reactor and primary coolant system of WWER-1200.
Source: gidropress.podolsk.ru
used with permission of АО ОКБ “ГИДРОПРЕСС”

In typical modern pressurized water reactors (PWRs), the Reactor Coolant System (RCS), shown in the figure, consists of:

All RCS components are located inside the containment building.

There is compressed liquid water inside the reactor vessel, loops, and steam generators at normal operation.  The pressure is maintained at approximately 16MPa. At this pressure, water boils at approximately 350°C (662°F).  The inlet temperature of the water is about 290°C (554°F). The water (coolant) is heated in the reactor core to approximately 325°C (617°F) as the water flows through the core. As it can be seen, the reactor contains approximately 25°C subcooled coolants (distance from the saturation).volume-of-reactor-coolant-system This high pressure is maintained by the pressurizer, a separate vessel that is connected to the primary circuit (hot leg) and partially filled with water (partially with saturated steam) which is heated to the saturation temperature (boiling point) for the desired pressure by submerged electrical heaters. The temperature in the pressurizer can be maintained at 350 °C. About 60% of the pressurizer volume occupies the compressed water at normal conditions, and about 40% of the volume occupies the saturated steam.

Volumes of typical PWR are in the following table.

It is an illustrative example, and the following data do not correspond to any reactor design.

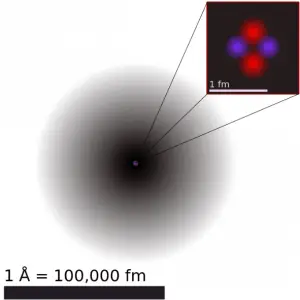
It must be noted the volume of the coolant significantly changes with the temperature of the coolant. The total mass of the coolant always remains the same. A change in water volume is not a change in water inventory. The reactor coolant volume changes with temperature because of changes in density. Most substances expand when heated and contract when cooled. However, the amount of expansion or contraction varies, depending on the material. This phenomenon is known as thermal expansion. The change in volume of a material that undergoes a temperature change is given by the following relation:

thermal-expansion

where ∆T is the temperature change, V is the original volume, ∆V is the volume change, and αV is the coefficient of volume expansion.

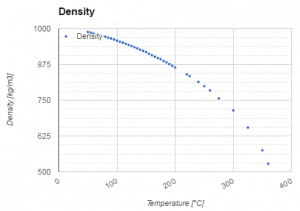
Chart - density - water - temperature
The density of liquid (compressed) water as a function of the temperature of the water

The volumetric thermal expansion coefficient for water is not constant over the temperature range and increases with the temperature (especially at 300°C). Therefore the change in density is not linear with temperature (as indicated in the figure).

See also: Steam Tables.

At normal conditions, the total volume of coolant in the reactor coolant system is almost constant. On the other hand, during transient load conditions, the volume can significantly change. These changes are naturally reflected in a change in pressurizer water level. When the average temperature of reactor coolant goes down gradually, the total water volume also decreases, which lowers the pressurizer level. On a gradual load pick-up, the increase in the average temperature of reactor coolant causes the total water volume to expand, raising the pressurizer level. These effects must be controlled by a pressurizer level control system.

Control Volume – Control Volume Analysis

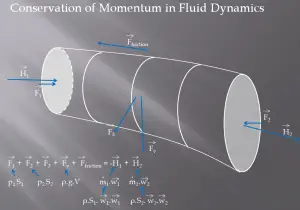Conservation of Momentum - FluidsA control volume is a fixed region in space chosen for the thermodynamic study of mass and energy balances for flowing systems. The boundary of the control volume may be a real or imaginary envelope. The control surface is the boundary of the control volume.

For example, a control volume analysis can be used to determine the rate of change of momentum for a fluid. This analysis will consider a stream tube (control volume) as we did for the Bernoulli equation. In this control volume, any change in momentum of the fluid within a control volume is due to the action of external forces on the fluid within the volume.

See also: Momentum Formula.

As can be seen from the picture, the control volume method can be used to analyze the law of conservation of momentum in the fluid. The control volume is an imaginary surface enclosing a volume of interest. The control volume can be fixed or moving, and it can be rigid or deformable. To determine all forces acting on the surfaces of the control volume, we have to solve the conservation laws in this control volume.

Choosing a Control Volume

A control volume can be selected as any arbitrary volume through which fluid flows. This volume can be static, moving, and even deforming during flow. To solve any problem, we have to solve basic conservation laws in this volume. It is very important to know all relative flow velocities to the control surface. Therefore it is very important to define exactly the boundaries of the control volume during an analysis.

Example: Water Jet Striking a Stationary Plate

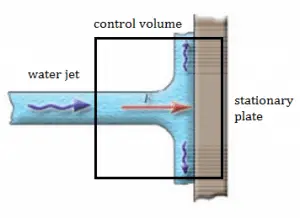Momentum Equation - Water JetA stationary plate (e.g.,, blade of a watermill) deflects water flow at a velocity of 1 m/s and an angle of 90°. It occurs at atmospheric pressure, and the mass flow rate is equal to Q =1 m3/s.

  1. Calculate the pressure force.
  2. Calculate the body force.
  3. Calculate the total force.
  4. Calculate the resultant force.

Solution

  1. The pressure force is zero as the pressure at the inlet, and the outlets to the control volume are atmospheric.
  2. As the control volume is small, we can ignore the body force due to the weight of gravity.
  3. Fx = ρ.Q.(w1x – w2x) = 1000 . 1 . (1 – 0) = 1000 N
    Fy = 0
    F = (1000, 0)
  4. The resultant force on the plane is the same magnitude but in the opposite direction as the total force F (friction and weight are neglected).

h
The water jet exerts on the plate the force of 1000 N in the x-direction.

 
References:
Reactor Physics and Thermal Hydraulics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. Todreas Neil E., Kazimi Mujid S. Nuclear Systems Volume I: Thermal Hydraulic Fundamentals, Second Edition. CRC Press; 2 edition, 2012, ISBN: 978-0415802871
  6. Zohuri B., McDaniel P. Thermodynamics in Nuclear Power Plant Systems. Springer; 2015, ISBN: 978-3-319-13419-2
  7. Moran Michal J., Shapiro Howard N. Fundamentals of Engineering Thermodynamics, Fifth Edition, John Wiley & Sons, 2006, ISBN: 978-0-470-03037-0
  8. Kleinstreuer C. Modern Fluid Dynamics. Springer, 2010, ISBN 978-1-4020-8670-0.
  9. U.S. Department of Energy, THERMODYNAMICS, HEAT TRANSFER, AND FLUID FLOW. DOE Fundamentals Handbook, Volume 1, 2, and 3. June 1992.

See above:

Thermodynamic Properties