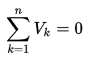Facebook Instagram Youtube Twitter

Electrical Energy

Electrical energy is the energy derived from electric potential energy or kinetic energy. A typical nuclear power plant has an electric-generating capacity of 1000 MWe. It produces 1 000 000 000 joules of electrical energy per second. The heat source in the nuclear power plant is a nuclear reactor. As is typical in all conventional thermal power stations, the heat is used to generate steam which drives a steam turbine connected to a generator that produces electricity. The turbines are heat engines subject to the efficiency limitations imposed by the second law of thermodynamics. In modern nuclear power plants, the overall thermodynamic efficiency is about one-third (33%), so 3000 MWth of thermal power from the fission reaction is needed to generate 1000 MWe of electrical power.

Since voltage is electric potential energy per unit charge, Kirchhoff’s voltage law can be seen to be a consequence of the conservation of electrical energy. Kirchhoff’s voltage law states:

The algebraic sum of the voltages (drops or rises) encountered in traversing any loop of a circuit in a specified direction must be zero.

The algebraic sum of the voltages (drops or rises) encountered in traversing any loop of a circuit in a specified direction must be zero.

kirchhoffs-voltage-law-equation1

The voltage changes around any closed loop must sum to zero. The sum of the voltage rises is equal to the sum of the voltage drops in a loop. No matter what path you take through an electric circuit, if you return to your starting point, you must measure the same voltage, constraining the net change around the loop to be zero. This rule is equivalent to saying that each point on a mountain has only one elevation above sea level. If you start from any point and return to it after walking around the mountain, the algebraic sum of the elevation changes that you encounter must be zero.

Energy Units

Energy is generally defined as the potential to do work or produce heat. This definition causes the SI unit for energy to be the same as the unit of work – the joule (J). Joule is a derived unit of energy, and it is named in honor of James Prescott Joule and his experiments on the mechanical equivalent of heat. In more fundamental terms, 1 joule is equal to:

1 J = 1 kg.m2/s2

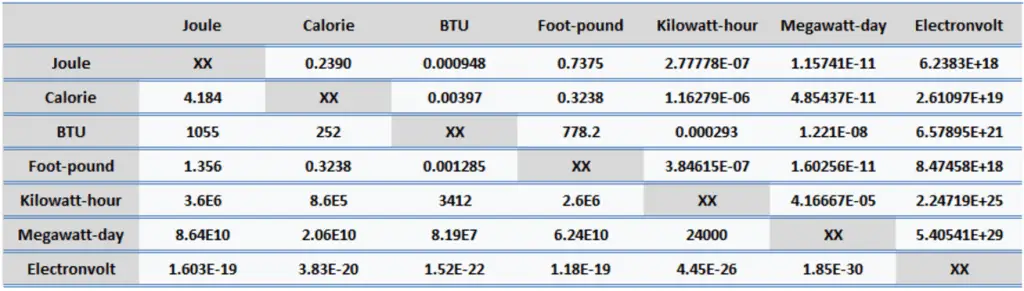
Since energy is a fundamental physical quantity used in various branches of physics and engineering, there are many units in physics and engineering. These units are summarized in following points:

 
Joule (unit: J)
Joule (unit: J). Joule is a derived unit of energy. It is equal to the energy transferred to an object when a force of one newton acts on that object in the direction of its motion through a distance of one meter.
    • 1 joule = 0.239 Calories
    • 1 joule = 9.48 x 10-4 BTU
    • 1 joule = 2.778 x 10-7 kWh

conversion - joule, calorie, kilowatthour - energy units

Examples of Energy of 1 Joule:

One joule in everyday life and science corresponds to approximately:

  • The kinetic energy of an object with mass 1 kg moving at √2 ≈ 1.4 m/s.
  • The kinetic energy of a 50 kg object (e.g.,, human) moving very slowly – approximately 0.72 km/h.
  • The energy required to lift a medium-size apple (100 g) 1 meter vertically from the surface of the Earth.
  • The heat required to raise the temperature of 1 g of water by 0.24 °C.
  • The heat required to evaporate of 0.00044 g of liquid water at 100°C.
  • The amount of electricity required to light a 1 watt LED for 1 s.
  • Is released by approximately 3.1⋅1010 fissions in a nuclear reactor.
Kilowatt-hour (unit: kWh)
Kilowatt-hour (unit: kWh). Kilowatt-hour is a derived unit of energy. It is used to measure energy, especially electrical energy in commercial applications. One kilowatt-hour is equal to one kilowatt of power produced or consumed over a period of one hour (kilowatts multiplied by the time in hours). Electric utilities commonly use the kilowatt-hour as a billing unit for energy delivered to consumers. 1kW . h = 1kW . 3600s = 3600kWs = 3600kJ = 3600000J. One kilowatt-hour corresponds to the heat required to evaporate 1.58 kg of liquid water at 100°C. A radio rated at 100 watts operating for 10 hours continuously uses one-kilowatt hour.
    • 1 kWh = 3.6 x 106 J
    • 1 kWh = 8.6 x 105 cal
    • 1 kWh = 3412 BTU

conversion - joule, calorie, kilowatthour - energy units

 
References:
Reactor Physics and Thermal Hydraulics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. Todreas Neil E., Kazimi Mujid S. Nuclear Systems Volume I: Thermal Hydraulic Fundamentals, Second Edition. CRC Press; 2 edition, 2012, ISBN: 978-0415802871
  6. Zohuri B., McDaniel P. Thermodynamics in Nuclear Power Plant Systems. Springer; 2015, ISBN: 978-3-319-13419-2
  7. Moran Michal J., Shapiro Howard N. Fundamentals of Engineering Thermodynamics, Fifth Edition, John Wiley & Sons, 2006, ISBN: 978-0-470-03037-0
  8. Kleinstreuer C. Modern Fluid Dynamics. Springer, 2010, ISBN 978-1-4020-8670-0.
  9. U.S. Department of Energy, THERMODYNAMICS, HEAT TRANSFER, AND FLUID FLOW. DOE Fundamentals Handbook, Volume 1, 2, and 3. June 1992.

See above:

Energy