The entropy can be made into an intensive or specific, variable by dividing by the mass. Engineers use the specific entropy in thermodynamic analysis more than the entropy itself. The specific entropy (s) of a substance is its entropy per unit mass. It equals the total entropy (S) divided by the total mass (m).
s = S/m
where:
s = specific entropy (J/kg)
S = entropy (J)
m = mass (kg)
Entropy quantifies the energy of a substance that is no longer available to perform useful work. Because entropy tells so much about the usefulness of an amount of heat transferred in performing work, the steam tables include values of specific entropy (s = S/m) as part of the information tabulated.
In general, specific entropy is a property of a substance, like pressure, temperature, and volume, but it cannot be measured directly. Normally, the entropy of a substance is given for some reference value. For example, the specific entropy of water or steam is given using the reference that the specific entropy of water is zero at 0.01°C and normal atmospheric pressure, where s = 0.00 kJ/kg. The absolute value of specific entropy is unknown is not a problem, however, because it is the change in specific entropy (∆s) and not the absolute value that is important in practical problems.
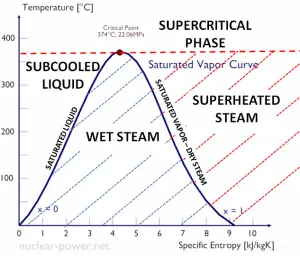
Temperature-entropy Diagrams – T-s Diagrams
The phases of a substance and the relationships between its properties are most commonly shown on property diagrams. A large number of different properties have been defined, and there are some dependencies between properties.
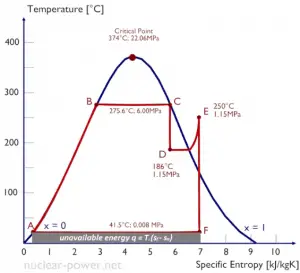
A Temperature-entropy diagram (T-s diagram) is the type of diagram most frequently used to analyze energy transfer system cycles. It is used in thermodynamics to visualize changes to temperature and specific entropy during a thermodynamic process or cycle.
The work done by or on the system and the heat added to or removed from the system can be visualized on the T-s diagram. By the definition of entropy, the heat transferred to or from a system equals the area under the T-s curve of the process.
dQ = TdS
An isentropic process is depicted as a vertical line on a T-s diagram, whereas an isothermal process is horizontal. In an idealized state, compression is a pump, compression in a compressor, and expansion in a turbine is isentropic processes. Therefore it is very useful in power engineering, because these devices are used in thermodynamic cycles of power plants.
Note that, the isentropic assumptions are only applicable with ideal cycles. Real thermodynamic cycles have inherent energy losses due to inefficiency of compressors and turbines.
The specific entropy is included in the steam tables for pure substances like steam, similar to a specific volume, specific internal energy, and specific enthalpy.
The specific entropy of saturated liquid water (x=0) and dry steam (x=1) can be picked from steam tables. In case of wet steam, the actual entropy can be calculated with the vapor quality, x, and the specific entropies of saturated liquid water and dry steam:
swet = ss x + (1 – x ) sl
where
swet = entropy of wet steam (J/kg K)
ss = entropy of “dry” steam (J/kg K)
sl = entropy of saturated liquid water (J/kg K)