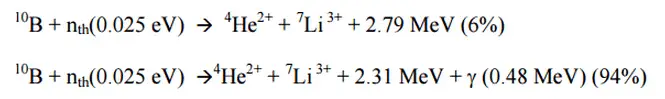By absorbing neutrons, a control rod prevents the neutrons from causing further fissions. Control rods are an important safety system for nuclear reactors. Their prompt action and prompt response to the reactor are indispensable. Control rods are used for maintaining the desired state of fission reactions within a nuclear reactor (i.e., subcritical state, critical state, power changes). They constitute a key component of an emergency shutdown system (SCRAM).

Source: www.gidropress.podolsk.ru/files/proceedings
/mntk2011/documents/mntk2011-108.pdf
Control rods usually constitute cluster control rod assemblies (PWR) inserted into guide thimbles within a nuclear fuel assembly. The cladding protects the absorbing material (e.g.,, pellets of Boron Carbide), usually made of stainless steel. They are grouped into groups (banks), and the movement usually occurs by the groups (banks). The typical total number of clusters is 70. This number is limited, especially by the number of penetrations of the reactor pressure vessel head.
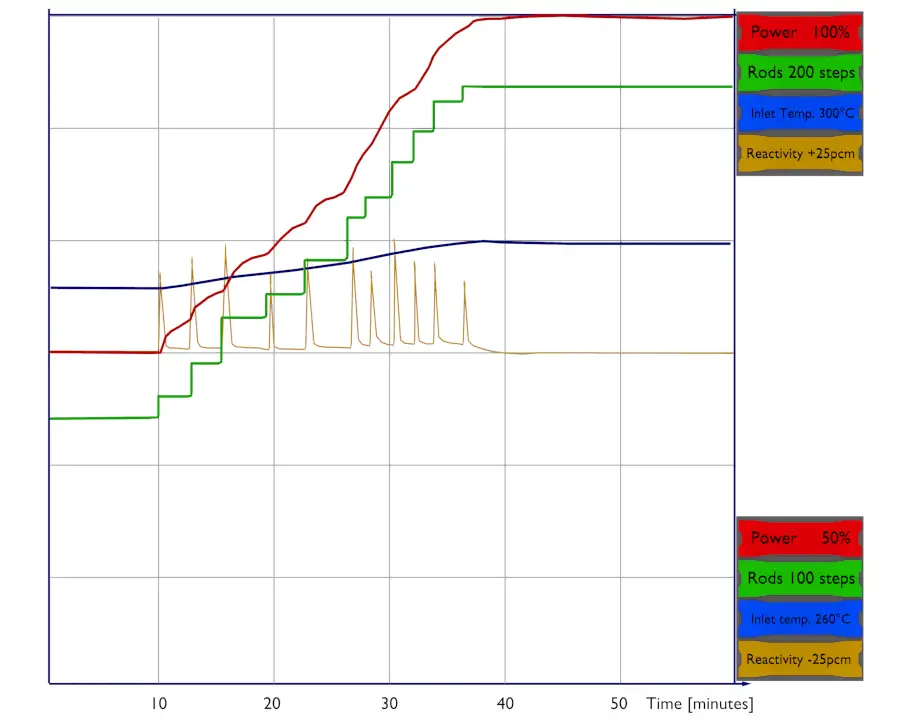
A control rod is removed from or inserted into the reactor core to increase or decrease the reactor’s reactivity (increase or decrease the neutron flux). By the changes of the reactivity, the changes of neutron power are performed. This, in turn, affects the reactor’s thermal power, the amount of steam produced, and hence the electricity generated.
In PWRs, they are inserted from above, with the control rod drive mechanisms being mounted on the reactor pressure vessel head. Due to the necessity of a steam dryer above the core of a boiling water reactor, this design requires the insertion of the control rods from underneath the core.
Control Rods usage
- Reactor startup.
- Control of the reactor and power maneuvering.
- Axial offset control.
- Reactor shutdown.
- Emergency shutdown – SCRAM.
Grey control rods
Some nuclear power plants use load following. These plants have the capability to make power maneuvering between 30% and 100% of rated power, with a slope up to 5% of rated power per minute. They can respond very quickly to the grid requirements. Special control rods have to be used to fulfill these requirements without introducing a large perturbation of the power distribution. These control rods are called “grey” control rods. Grey control rods use a grey neutron absorber, which absorbs fewer neutrons than a “black” absorber. Consequently, they cause smaller depressions in the neutron flux and power in the vicinity of the rod.
How to control the reactor power?
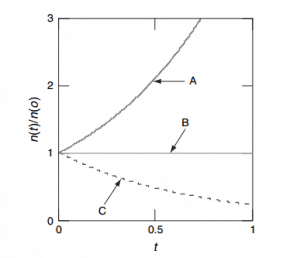
The reactor’s thermal power is determined by the number of fission reactions per time unit and by remaining decay heat (~tens of MW). During the normal operation of the reactor, the thermal power from fission dominates. The neutron flux determines the number of fission reactions in the reactor. The position of control rods directly affects the criticality of the reactor. When the reactor is critical (control rods in a critical position), the reactor’s power and the neutron flux are stable at a given power level. When the reactor is subcritical (control rods below a critical position), the reactor’s power and the neutron flux exponentially decrease. When the reactor is supercritical (control rods above a critical position), the reactor’s power and the neutron flux exponentially increase. It should be noted this behavior describes “zero power criticality” (i.e., a reactor without reactivity feedbacks, 10E-8% – 1% of rated power).
Criticality of a Power Reactor
For power reactors, the reactor can behave differently at power conditions due to the presence of reactivity feedbacks. Power reactors are initially started from hot standby mode (a subcritical state at 0% of rated power) to power operation mode (100% of rated power) by withdrawing control rods and boron dilution from the primary source coolant. During the reactor startup and up to about 1% of rated power, the reactor kinetics is exponential as in a zero-power reactor. This is due to the fact all temperature reactivity effects are minimal.
On the other hand, temperature reactivity plays a very important role during further power increase from about 1% up to 100% of rated power. As the neutron population increases, the fuel and the moderator increase their temperature, which results in a decrease in reactivity of the reactor (almost all reactors are designed to have the temperature coefficients negative).
The negative reactivity coefficient acts against the initial positive reactivity insertion, and this positive reactivity is offset by negative reactivity from temperature feedbacks. Positive reactivity must be continuously inserted (via control rods or chemical shim) to keep the power increasing. After each reactivity insertion, the reactor power stabilizes itself on the power level proportionately to the reactivity inserted.
See also: Reactor Criticality.
Accident-tolerant control rods – ATCR
Control rods are an important safety system of nuclear reactors. Their prompt action and prompt response to the reactor are indispensable. Control rods are used for maintaining the desired state of fission reactions within a nuclear reactor (i.e., subcritical state, critical state, power changes). They constitute a key component of an emergency shutdown system (SCRAM).
Control rods are rods, plates, or tubes containing a neutron absorbing material (material with high absorption cross-section for thermal neutron) such as boron, hafnium, cadmium, etc., used to control the power of a nuclear reactor. By absorbing neutrons, a control rod prevents the neutrons from causing further fissions.
Control rods usually constitute cluster control rod assemblies (PWR) inserted into guide thimbles within a nuclear fuel assembly. The cladding protects the absorbing material (e.g.,, Boron Carbide or Ag-In-Cd alloy), usually made of stainless steel.
Nevertheless, the melting point of Ag-In-Cd alloy (~790 ̊C), the eutectic temperature of boron carbide (B4C) and Fe (~1150 ̊C), and the eutectic temperature of Fe and Zr (~950 ̊C) are lower than the temperature (≳1 200) at which Zr-alloy fuel cladding begins to be intensively oxidized under severe accident conditions. Accordingly, the control rods may melt and collapse before the reactor core is significantly damaged in the case of severe accidents.
The following inherent characteristics are required in accident tolerant control rods:
- The reactivity worth of ATCR should be comparable to or exceed that of conventional CR.
- The neutron-absorbing materials used in ATCR should have a sufficiently high melting point and high eutectic temperature with cladding to prevent CR breakage from extensive fuel rod failure in a severe accident, thus avoiding uncontrollable recriticality even if coolant without boron is injected for emergency cooling of the core.
The main idea is to replace the conventional neutron-absorbing materials with proper ceramic materials that satisfy the above requirements. The candidate of a new absorber material for ATC includes gadolinium (Gd2O3), samarium (Sm2O3), europium (Eu2O3), dysprosium (Dy2O3), hafnia (HfO2). The melting point of these materials and the liquefaction temperature with Fe are higher than the rapid zirconium alloy oxidation temperature.