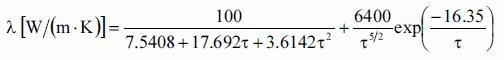Fuel Pellets

Temperature Profile – Fuel Pellets

See also: Temperature Profile – Calculation

See also: Cladding Surface Temperature

See also: Thermal Conduction of Uranium Dioxide

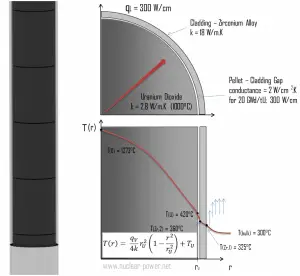The thermal and mechanical behavior of fuel pellets and fuel rods constitute one of three key core design disciplines. Nuclear fuel is operated under very inhospitable conditions (thermal, radiation, mechanical) and must withstand more than normal conditions operation. For example, temperatures in the center of fuel pellets reach more than 1000°C (1832°F), accompanied by fission-gas releases. Therefore detailed knowledge of temperature distribution within a single fuel rod is essential for the safe operation of nuclear fuel. In this section, we will study the heat conduction equation in cylindrical coordinates using the Dirichlet boundary condition with a given surface temperature (i.e., using the Dirichlet boundary condition). A separate section will study a comprehensive analysis of the fuel rod temperature profile.

Enthalpy of Nuclear Fuel

Enthalpy of nuclear fuel is also used as an acceptance criterion in very specific types of accidents, known as reactivity-initiated accidents (RIA), such as Rod Ejection Accidents. RIAs consist of postulated accidents involving a sudden and rapid positive reactivity insertion. As a result of rapid power excursion, fuel temperatures rapidly increase, prompting fuel pellet thermal expansion. The power excursion is initially mitigated by the fuel temperature coefficient (or Doppler feedback), which will be the first feedback that will compensate for the inserted positive reactivity.

In these accidents, the large and rapid energy deposition in the fuel can result in melting, fragmentation, and dispersal of fuel. The mechanical action associated with fuel dispersal can be sufficient to destroy the fuel’s cladding and rod-bundle geometry and produce pressure pulses in the primary system. The expulsion of hot fuel into the water can cause rapid steam generation and these pressure pulses, which could damage nearby fuel assemblies. Limits on specific fuel enthalpy are used because the experimental tests show that the degree of fuel rod damage correlates well with the peak value of fuel pellet-specific enthalpy.

Regulatory acceptance criteria vary with country and reactor type, but there are usually two kinds of fuel enthalpy limits:

1. CORE COOLABILITY CRITERIA. Reduction of coolability can result from violent expulsion of fuel, which could damage nearby fuel assemblies. In the past, the core coolability criteria were revised to address short-term specifically (e.g., fuel-to-coolant interaction, rod burst) and long-term (e.g., fuel rod ballooning, flow blockage) phenomena that challenge coolable geometry and reactor pressure boundary integrity. A definite limit for core damage, which must not be exceeded at any position in any fuel rod in the core. According to Appendix B of the Standard Review Plan, Section 4.2, these criteria are, for example:
   1. Peak radial average fuel enthalpy must remain below 230 cal/g. Above this enthalpy, hot fuel particles might be expelled from a fuel rod.
   2. Peak fuel temperature must remain below incipient fuel melting conditions.
2. FUEL CLADDING FAILURE CRITERIA. A fuel rod failure threshold defines whether a fuel rod should be considered as failed or not in calculations of radioactive release (source term). According to Appendix B of the Standard Review Plan, Section 4.2 fuel rods may fail by several damage mechanisms:
   1. The high cladding temperature failure criteria for zero power conditions is a peak radial average fuel enthalpy greater than 170 cal/g for fuel rods with an internal rod pressure at or below system pressure and 150 cal/g for fuel rods with an internal rod pressure exceeding system pressure.
   2. The PCMI failure criteria is a change in radial average fuel enthalpy greater than the corrosion-dependent limit depicted in Appendix B of the Standard Review Plan, Section 4.2.

See also: Enthalpy of Nuclear Fuel

Fuel – Cladding Gap

There is also one very important phenomenon that influences the fuel temperature. As the fuel burnup increases, the fuel-cladding gap reduces. This reduction is caused by the swelling of the fuel pellets and cladding creep. Fuel pellet swelling occurs because fission gases cause the pellet to swell, resulting in a larger pellet volume. At the same time, the cladding is distorted by outside pressure (known as the cladding creep). These two effects result in direct fuel-cladding contact (e.g., at burnup of 25 GWd/tU). The direct fuel-cladding contact causes a significant reduction in fuel temperature profile because the overall thermal conductivity increases due to conductive heat transfer.

Fuel Burnup and High Burnup Structure

In nuclear engineering, fuel burnup (also known as fuel utilization) measures how much energy is extracted from nuclear fuel and measures fuel depletion. Reactor engineers distinguish between:

• Core Burnup. Averaged burnup over the entire core (i.e., overall fuel assemblies). For example – BU_core = 25 000 MWd/tHM
• Fuel Assembly Burnup. Averaged burnup over single assembly  (i.e., overall fuel pins of a single fuel assembly). For example – BU_FA = 40 000 MWd/tHM
• Pin Burnup. Averaged burnup over a single fuel pin or fuel rod (overall fuel pellets of a single fuel pin). For example – BU_pin = 45 000 MWd/tHM
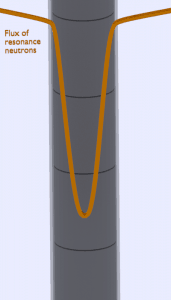
• Local or Fine Mesh Burnup. Burnup significantly varies also within a single fuel pellet. For example, the local burnup at the rim of the UO₂ pellet can be 2–3 times higher than the average pellet burnup. This local anomaly causes the formation of a structure known as a High Burnup Structure.

The distribution of heat generation is not homogeneous across the pellet. Indeed, the generation of Pu 239 by capture, in uranium 238, of epithermal neutrons is quite marked in the pellet rim by way of the self-shielding effect (for neutrons endowed with an energy corresponding to resonances, the capture cross-section is so large that they are unable to reach the center of the pellet). This overconcentration of plutonium in the rim, gradually building up during irradiation, results in a drop, from rim to center, in radial power distribution. Therefore local burnup significantly varies also within a single fuel pellet. For example, the local burnup at the rim of the UO² pellet can be 2–3 times higher than the average pellet burnup. This local anomaly causes the formation of a microstructure known as a High Burnup Structure.

Uranium Dioxide – UO2

Uranium dioxide is a ceramic refractory uranium compound, in many cases, used as a nuclear fuel. Most LWRs use uranium fuel in the form of uranium dioxide (chemically UO₂). Uranium dioxide is a black semiconducting solid with very low thermal conductivity. On the other hand, uranium dioxide has a very high melting point and has well-known behavior.

Uranium dioxide has a significantly lower density than uranium in metal form. Uranium dioxide has a density of 10.97 g/cm³, but this value may vary with fuel burnup because, at low burnup, densification of pellets can occur, and at higher burnup, swelling occurs.

Thermal Conductivity of Uranium Dioxide

See also: Thermal Conduction of Uranium Dioxide

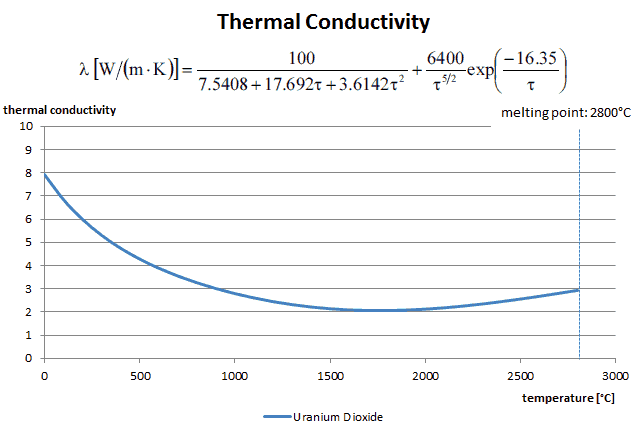
The thermal conductivity of uranium dioxide is very low compared to metal uranium, uranium nitride, uranium carbide, and zirconium cladding material. Thermal conductivity is one of the parameters determining the fuel centerline temperature. This low thermal conductivity can result in localized overheating in the fuel centerline; therefore, this overheating must be avoided. Overheating of the fuel is prevented by maintaining the steady state peak linear heat rate (LHR) or the Heat Flux Hot Channel Factor – F_Q(z) below the level at which fuel centerline melting occurs. Expansion of the fuel pellet upon centerline melting may cause the pellet to stress the cladding to the point of failure.

Thermal conductivity of solid UO₂ with a density of 95% is estimated by the following correlation [Klimenko; Zorin]:

where τ = T/1000. The uncertainty of this correlation is +10% in the range from 298.15 to 2000 K and +20% in the range from 2000 to 3120 K.

Special reference: Thermal and Nuclear Power Plants/Handbook ed. by A.V. Klimenko and V.M. Zorin. MEI Press, 2003.

Special reference: Thermophysical Properties of Materials For Nuclear Engineering: A Tutorial and Collection of Data. IAEA-THPH, IAEA, Vienna, 2008. ISBN 978–92–0–106508–7.

Advanced Fuel Pellets

 According to the NEA report, the fuel designs covered by the Task Force on Advanced Fuel Designs consist of three different concepts:

• Improved UO2 fuel. Regarding the improved UO2 fuel, this design was divided into two sub-concepts: oxide-doped UO2 and high-thermal conductivity UO2 (designed by adding metallic or ceramic dopant).
• High-density fuel.
• Encapsulated fuel (TRISO-SiC-composite pellets).