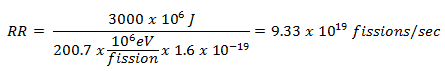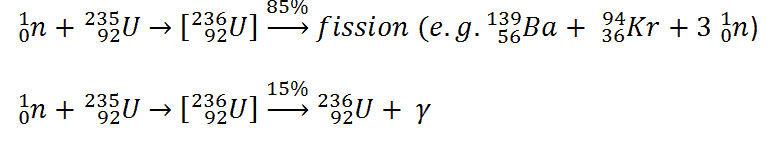A typical nuclear power plant has an electric-generating capacity of 1000 MWe. The heat source in the nuclear power plant is a nuclear reactor. As is typical in all conventional thermal power stations, the heat is used to generate steam which drives a steam turbine connected to a generator that produces electricity. The turbines are heat engines subject to the efficiency limitations imposed by the second law of thermodynamics. In modern nuclear power plants, the overall thermodynamic efficiency is about one-third (33%), so 3000 MWth of thermal power from the fission reaction is needed to generate 1000 MWe of electrical power.
This thermal power is generated in a reactor core, which contains especially the nuclear fuel (fuel assemblies), the moderator, and the control rods. The reactor’s core contains all the nuclear fuel assemblies and generates most of the heat (fraction of the heat is generated outside the reactor – e.g.,, gamma rays energy). The assemblies are exactly placed in the reactor according to a fuel loading pattern.
A typical 1000 MWe (3000 MWth) nuclear core may contain 157 fuel assemblies composed of over 45,000 fuel rods and 15 million fuel pellets. Generally, a common fuel assembly contains energy for approximately 4 years of operation at full power. Once loaded, the fuel stays in the core for 4 years, depending on the design of the operating cycle. During these 4 years, the reactor core has to be refueled. During refueling, every 12 to 18 months, some of the fuel – usually one-third or one-quarter of the core – is removed to the spent fuel pool. At the same time, the remainder is rearranged to a location in the core better suited to its remaining level of enrichment. The removed fuel (one-third or one-quarter of the core, i.e., 40 assemblies) must be replaced by fresh fuel assemblies. It follows, there are about 3-4 fuel batches that differ from each other in the fuel burnup.
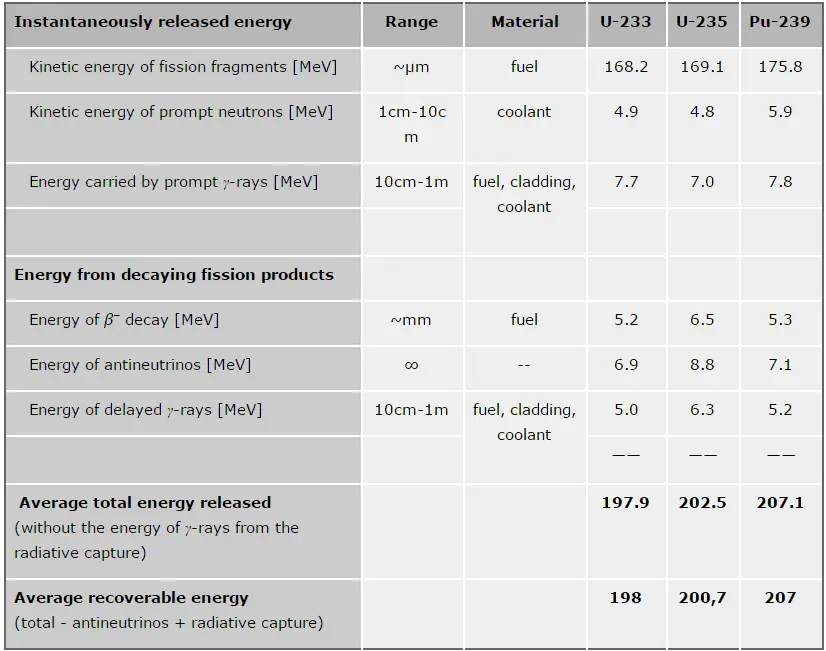
The total energy released in a reactor is about 210 MeV per 235U fission, distributed as shown in the table. In a reactor, the average recoverable energy per fission is about 200 MeV, being the total energy minus the energy of antineutrinos that are radiated away. This means that about 3.1⋅1010 fissions per second are required to produce a thermal power of 1 W. Since 1 gram of any fissile material contains about 2.5 x 1021 nuclei, the fissioning of 1 gram of fissile material yields about 1 megawatt-day (MWd) of heat energy.
Summary:
Consumption of a 3000MWth (~1000MWe) reactor (12-months fuel cycle)
It is an illustrative example, and the following data do not correspond to any reactor design.
- A typical reactor may contain about 165 tonnes of fuel (including structural material)
- A typical reactor may contain about 100 tonnes of enriched uranium (i.e., about 113 tonnes of uranium dioxide).
- This fuel is loaded within, for example, 157 fuel assemblies composed of over 45,000 fuel rods.
- A common fuel assembly contains energy for approximately 4 years of operation at full power.
- Therefore about one-quarter of the core is yearly removed to the spent fuel pool (i.e., about 40 fuel assemblies). At the same time, the remainder is rearranged to a location in the core better suited to its remaining level of enrichment (see Power Distribution).
- The removed fuel (spent nuclear fuel) still contains about 96% of reusable material (it must be removed due to decreasing kinf of an assembly).
- The annual natural uranium consumption of this reactor is about 250 tonnes of natural uranium (to produce about 25 tonnes of enriched uranium).
- The annual enriched uranium consumption of this reactor is about 25 tonnes of enriched uranium.
- The annual fissile material consumption of this reactor is about 1 005 kg.
- The annual matter consumption of this reactor is about 1.051 kg.
- But it corresponds to about 3 200 000 tons of coal burned in coal-fired power plant per year.
Uranium 235 consumption in a nuclear reactor
A typical thermal reactor contains about 100 tons of uranium with an average enrichment of 2% (do not confuse it with the enrichment of the fresh fuel, that is about 4%). For the reactor of power of 3000MWth, determine the consumption of 235U that must undergo fission each day to provide this thermal power.
Solution:
This problem can be solved very simply. The average recoverable energy per 235U fission is about Er = 200.7 MeV/fission. Since we know that each second we need 3000 MJ of energy, the required reaction rate can be determined directly as:
Since each atom of 235U has a mass of 235u x 1.66 x 10-27 kg/u = 3.9 x 10-25 kg, the daily consumption of a reactor is:
9.33 x 1019 fissions/sec x 3.9 x 10-25 kg x 86400 sec/day = 3.14 kg/day
For comparison, a 1000 MWe coal-fired power plant burns about 10 000 tons (about 10 million kg) of coal per day.
Since a typical fuel cycle takes about 320 days (12-month fuel cycle), the annual fuel consumption is about:
3.14 kg/day x 320 days = 1 005 kg of 235U
Typically, when uranium 235 nucleus undergoes fission, the nucleus splits into two smaller nuclei (triple fission can also rarely occur), along with a few neutrons (the average is 2.43 neutrons per fission by thermal neutron) and release of energy in the form of heat and gamma rays. The average of the fragment atomic mass is about 118, but very few fragments near that average are found. It is much more probable to break up into unequal fragments, and the most probable fragment masses are around mass 95 (Krypton) and 137 (Barium). Most fission fragments are highly unstable(radioactive) nuclei and undergo further radioactive decays to stabilize themselves.
Energy Release per Fission
In general, nuclear fission results in the release of enormous quantities of energy. The amount of energy depends strongly on the nucleus to be fissioned and also depends strongly on the kinetic energy of an incident neutron. It is necessary to identify the individual components of this energy precisely to calculate the power of a reactor. At first, it is important to distinguish between the total energy released and the energy that can be recovered in a reactor.
The total energy released in fission can be calculated from binding energies of the initial target nucleus to be fissioned and binding energies of fission products. But not all the total energy can be recovered in a reactor. For example, about 10 MeV is released in the form of neutrinos (in fact, antineutrinos). Since the neutrinos are weakly interacting (with an extremely low cross-section of any interaction), they do not contribute to the energy that can be recovered in a reactor.
See also: Energy Release from Fission
Fissile material consumption in a nuclear reactor
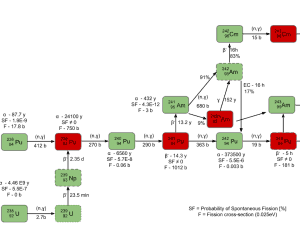All commercial light water reactors contain both fissile and fertile materials. For example, most PWRs use low enriched uranium fuel with enrichment of 235U up to 5%. Therefore more than 95% of the content of fresh fuel is fertile isotope 238U.
In fact, during fuel burnup, the fertile materials (conversion of 238U to fissile 239Pu known as fuel breeding) partially replace fissile 235U, thus in a nuclear reactor, more fissile isotopes are involved in power generation. Since the 239Pu fission releases a very similar amount of energy, this example can be generalized to:
Annual consumption is 1 005 kg of all fissile material involved.
The fuel breeding permits power reactors to operate longer before the amount of fissile material decreases to the point where reactor criticality is no longer manageable.
The fuel breeding in the fuel cycle of all commercial light water reactors plays a significant role. In recent years, the commercial power industry has been emphasizing high-burnup fuels (up to 60 – 70 GWd/tU), typically enriched to higher percentages of 235U (up to 5%). As burnup increases, a higher percentage of the total power produced in a reactor is due to the fuel bred inside the reactor.
At a burnup of 30 GWd/tU (gigawatt-days per metric ton of uranium), about 30% of the total energy released comes from bred plutonium. At 40 GWd/tU, that percentage increases to about forty percent. This corresponds to a breeding ratio for these reactors of about 0.4 to 0.5. That means about half of the fissile fuel in these reactors is bred there. This effect extends the cycle length for such fuels to sometimes nearly twice what it would be otherwise. MOX fuel has a smaller breeding effect than 235U fuel and is thus more challenging and slightly less economical to use due to a quicker drop-off in reactivity through cycle life.
Natural uranium consumption in a nuclear reactor
Natural uranium refers to uranium with the same isotopic ratio as found in nature. It consists primarily of isotope 238U (99.28%). Therefore the atomic mass of the uranium element is close to the atomic mass of the 238U isotope (238.03u). Natural uranium also consists of two other isotopes: 235U (0.71%) and 234U (0.0054%). The abundance of isotopes in nature is caused by differences in the half-lives. All three naturally-occurring isotopes of uranium (238U, 235U, and 234U) are unstable. On the other hand, these isotopes (except 234U) belong to primordial nuclides because their half-life is comparable to the age of the Earth (~4.5×109 years for 238U).
Since natural uranium contains only 0.71% of fissile isotope 235U and most current power reactors require enriched uranium, this natural uranium must be enriched. The level of enrichment required depends on specific reactor design (e.g.,, PWRs and BWRs require 3% – 5% of 235U) and specific requirements of the nuclear power plant operator. Without required enrichment, these reactors cannot initiate and sustain a nuclear chain reaction for such a long period as 12 months (or more).
The enrichment process separates gaseous uranium hexafluoride into two streams, enriched to the required level and known as low-enriched uranium. The other stream is progressively depleted in U-235 and is called ‘tails’, or depleted uranium. Typically, to produce 1 kg of enriched uranium with 5% of 235U, about 10 kg of natural uranium is required with a byproduct of about 9 kg of depleted uranium. Therefore annual natural uranium consumption of 3000MWth reactor is about 250 tonnes of natural uranium (to produce about 25 tonnes of enriched uranium).
Matter consumption in a nuclear reactor
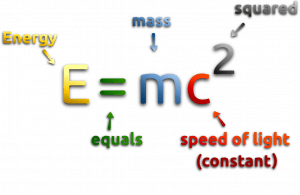In general, nuclear fission results in the release of enormous quantities of energy. This energy comes from the nuclear binding energy, which holds nuclei together. The binding energy per nucleon is higher for fission fragments than for uranium nuclei. It was found the sum of the rest masses of products of fission is measurably smaller than the rest mass of the uranium nucleus.
It is because, during nuclear fission, some of the mass of the nucleus gets converted into these huge amounts of energy, and thus this mass is removed from the total mass of the original particle. The mass is missing in the resulting nuclei.
According to the Einstein relationship (E = mc2), this binding energy is proportional to this mass difference, known as the mass defect.
The annual mass defect of a typical 3000MWth reactor can be calculated directly from the Einstein relationship (E = mc2) as:
Δm = ΔE/c2
Δm = 3000×106 (W = J/s) x 31.5×106 (seconds in year) / (2.9979 x 108)2 = 1.051 kg