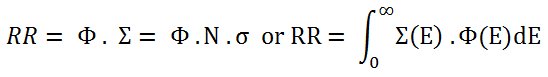In nuclear reactors, the thermal power produced by nuclear fissions is proportional to the neutron flux level. Therefore, from a reactor safety point of view, it is of the highest importance to measure and control the neutron flux and the spatial distribution of the neutron flux in the reactor correctly and by appropriate instrumentation. For this purpose, various nuclear instrumentations are installed. These measurements are usually performed outside the reactor core, but there are also measurements performed from inside the core. Therefore, nuclear instrumentations are usually categorized as:
-
- Excore Nuclear Instrumentation. The neutron flux is usually measured by excore neutron detectors installed outside the core. These detectors belong to the excore nuclear instrumentation system (NIS). Since the neutron flux covers a wide range (about 12 decades), three ranges of instrumentation are used to obtain accurate flux level measurements:
- Incore Nuclear Instrumentation. The incore nuclear instrumentation system measures neutron flux distribution and temperatures in the reactor core. The purposes of the incore instrumentation system are to provide detailed information on neutron flux distribution and fuel assembly outlet temperatures at selected core locations. The incore instrumentation system includes:
Both systems are based on the detection of neutrons. The neutron flux is usually measured by excore neutron detectors installed outside the core. These detectors belong to the so-called excore nuclear instrumentation system (NIS). The neutron flux and its distribution within the core are usually measured by an incore system installed inside the reactor. Although the nuclear instrumentation system provides a prompt response to neutron flux changes and it is an irreplaceable system, it must be calibrated. The accurate thermal power of the reactor can be measured only by methods based on the energy balance of the primary circuit or the energy balance of the secondary circuit. These methods provide accurate reactor power, but these methods are insufficient for safety systems. Signal inputs to these calculations are, for example, the hot leg temperature or the flow rate through the feedwater system, and these signals change very slowly with neutron power changes. In other words, the thermal power measured by colorimetric methods is accurate. In contrast, the nuclear power measured by excore neutron detectors is the only system capable of fast reactivity excursion detection.
Reaction Rate – Proportionality between Neutron Flux and Thermal Power
See also: Reaction Rate
Knowledge of the neutron flux (the total path length of all the neutrons in a cubic centimeter in a second) and the macroscopic cross sections (the probability of having an interaction per centimeter path length) allows us to compute the rate of interactions (e.g., rate of fission reactions). This reaction rate (the number of interactions taking place in that cubic centimeter in one second) is then given by multiplying them together:
where:
Ф – neutron flux (neutrons.cm-2.s-1)
σ – microscopic cross section (cm2)
N – atomic number density (atoms.cm-3)
The reaction rate for various types of interactions is found from the appropriate cross-section type:
-
-
- Σt . Ф – total reaction rate
- Σa . Ф – absorption reaction rate
- Σc. Ф – radiative capture reaction rate
- Σf. Ф – fission reaction rate
-
We must focus on the fission reaction rate to determine the thermal power. For simplicity, let’s assume that the fissionable material is uniformly distributed in the reactor. In this case, the macroscopic cross-sections are independent of position. Multiplying the fission reaction rate per unit volume (RR = Ф . Σ) by the total volume of the core (V) gives us the total number of reactions occurring in the reactor core per unit time. But we also know that the amount of energy released per one fission reaction is about 200 MeV/fission. It is possible to determine the rate of energy release (power) due to the fission reaction, and it is given by the following equation:
P = RR . Er . V = Ф . Σf . Er . V = Ф . NU235 . σf235 . Er . V
where:
P – reactor power (MeV.s-1)
Ф – neutron flux (neutrons.cm-2.s-1)
σ – microscopic cross section (cm2)
N – atomic number density (atoms.cm-3)
Er – the average recoverable energy per fission (MeV / fission)
V – total volume of the core (m3)