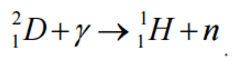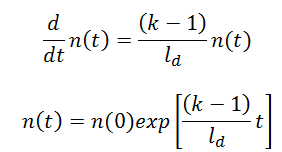It is known the fission neutrons are of importance in any chain-reacting system. Neutrons trigger the nuclear fission of some nuclei (235U, 238U, or even 232Th). What is crucial the fission of such nuclei produces 2, 3, or more free neutrons.
But not all neutrons are released at the same time following fission. Even the nature of the creation of these neutrons is different. From this point of view, we usually divide the fission neutrons into two following groups:
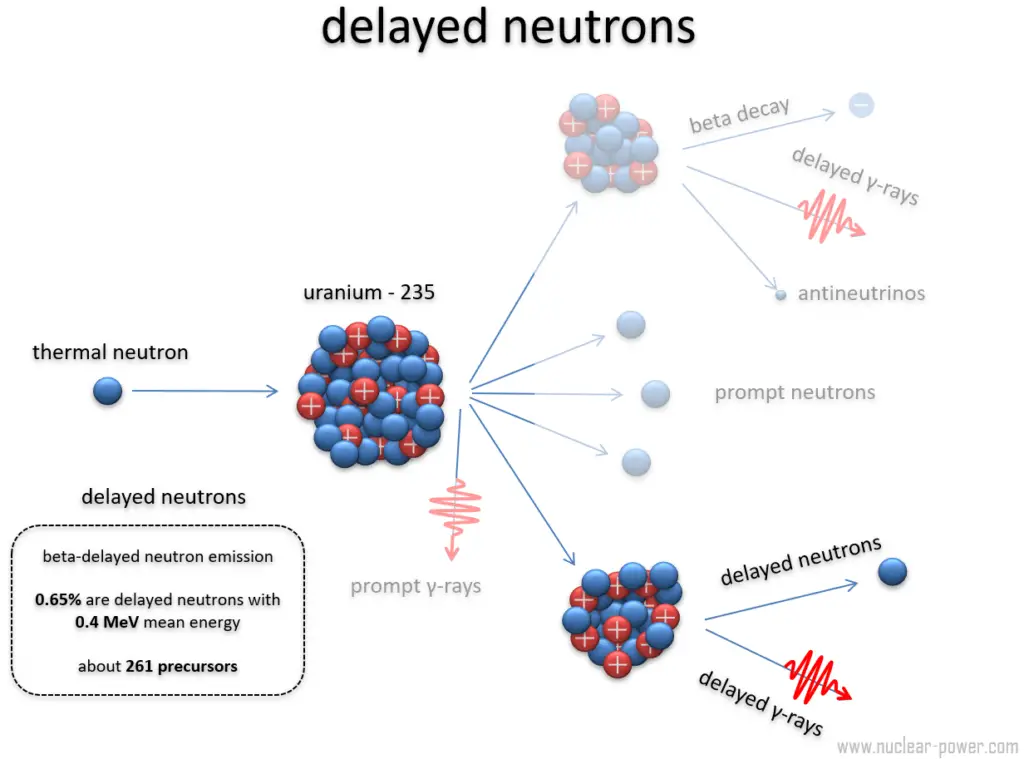
- Prompt Neutrons. Prompt neutrons are emitted directly from fission, and they are emitted within a very short time of about 10-14 seconds.
- Delayed Neutrons. Delayed neutrons are emitted by neutron-rich fission fragments that are called delayed neutron precursors. These precursors usually undergo beta decay, but a small fraction of them are excited enough to undergo neutron emission. The neutron is produced via this type of decay, and this happens orders of magnitude later than the emission of the prompt neutrons, which plays an extremely important role in the control of the reactor.
Delayed Neutrons
While most of the neutrons produced in fission are prompt neutrons, the delayed neutrons are important in reactor control. Delayed neutrons are perhaps the most important aspect of the fission process from the viewpoint of reactor control.
In this context, the term “delayed” means that the neutron is emitted with half-lives, ranging from few milliseconds up to 55 s for the longest-lived precursor 87Br. These neutrons have to be distinguished from the prompt neutrons, which are emitted immediately (on the order of 10-14 s) after a fission event from a neutron-rich nucleus. Although the amount of delayed neutrons is only on the order of tenths of a percent of the total amount, the timescale in seconds plays an extremely important role.
Key Characteristics of Delayed Neutrons
- The presence of delayed neutrons is perhaps the most important aspect of the fission process from reactor control.
- Delayed neutrons are emitted by neutron-rich fission fragments that are called delayed neutron precursors.
- These precursors usually undergo beta decay, but a small fraction of them are excited enough to undergo neutron emission.
- The emission of neutrons happens orders of magnitude later compared to the emission of the prompt neutrons.
- About 240 n-emitters are known between 8He and 210Tl. About 75 of them are in the non-fission region.
- It is suggested to group together the precursors based on their half-lives to simplify reactor kinetic calculations.
- Therefore delayed six delayed neutron groups traditionally represent neutrons.
- Neutrons can also be produced in (γ, n) reactions (especially in reactors with heavy water moderator), and therefore they are usually referred to as photoneutrons. Photoneutrons are usually treated no differently than regularly delayed neutrons in the kinetic calculations.
- The total yield of delayed neutrons per fission, vd, depends on:
- An isotope that is fissioned.
- The energy of a neutron induces fission.
- Variation among individual group yields is much greater than variation among group periods.
- In reactor kinetic calculations, it is convenient to use relative units as delayed neutron fraction (DNF).
- At the steady-state condition of criticality, with keff = 1, the delayed neutron fraction is equal to the precursor yield fraction β.
- In LWRs, the β decreases with fuel burnup. This is due to isotopic changes in the fuel.
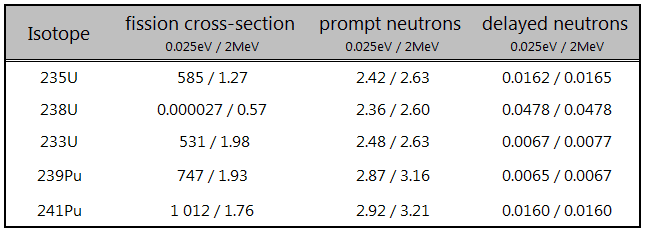
- Delayed neutrons have initial energy between 0.3 and 0.9 MeV with an average energy of 0.4 MeV.
- Depending on the type of the reactor, and their spectrum, the delayed neutrons may be more (in thermal reactors) or less effective than prompt neutrons (in fast reactors). The effectively delayed neutron fraction – βeff must be defined to include this effect in the reactor kinetic calculations.
- The effectively delayed neutron fraction is the product of the average delayed neutron fraction and the importance factor βeff = β . I.
- The weighted delayed generation time is given by τ = ∑iτi . βi / β = 13.05 s, therefore the weighted decay constant λ = 1 / τ ≈ 0.08 s-1.
- The mean generation time with delayed neutrons is about ~0.1 s, rather than ~10-5 as in section Prompt Neutron Lifetime, where the delayed neutrons were omitted.
- Their presence completely changes the dynamic time response of a reactor to some reactivity change, making it controllable by control systems such as the control rods.
Precursors of Delayed Neutrons
Delayed neutrons originate from the radioactive decay of nuclei produced in fission, and hence they are different for each fissile material. They are emitted by excited neutron-rich fission fragments (so-called the delayed neutron precursors) some appreciable time after the fission. How long afterward depends on the precursor’s half-life since the neutron emission occurs in a very short time. The precursors usually undergo beta decay without any neutron emission, but a small fraction of them (highly excited nuclei) can undergo the neutron emission instead of the gamma emission.
In addition, current nuclear physics facilities can produce more neutron-rich isotopes that can emit multiple neutrons. Currently, about 18 2n-emitters are experimentally confirmed [IAEA – INDC(NDS)-0599], but only two of them are fission products.
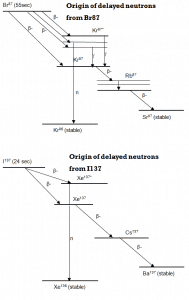 As an example, the isotope 87Br is the major component of the first group of precursor nuclei. This isotope has a half-life of 55.6 seconds. It undergoes negative beta decay through its two main branches with 2.6 MeV and 8 MeV beta particles emissions. This decay leads to the formation of 87Kr* and 87Kr (ground state), and the 87Kr nucleus subsequently decays via two successive beta decays into the stable isotope 87Sr. But there is also one possible way for the 87Br nucleus to beta decay. The 87Br nucleus can beta decay into an excited state of the 87Kr nucleus at an energy of 5.5 MeV, larger than the binding energy of a neutron in the 87Kr nucleus. In this case, the 87Kr nucleus can undergo (with the probability of 2.5%) a neutron emission, leading to a stable 87Kr isotope.
As an example, the isotope 87Br is the major component of the first group of precursor nuclei. This isotope has a half-life of 55.6 seconds. It undergoes negative beta decay through its two main branches with 2.6 MeV and 8 MeV beta particles emissions. This decay leads to the formation of 87Kr* and 87Kr (ground state), and the 87Kr nucleus subsequently decays via two successive beta decays into the stable isotope 87Sr. But there is also one possible way for the 87Br nucleus to beta decay. The 87Br nucleus can beta decay into an excited state of the 87Kr nucleus at an energy of 5.5 MeV, larger than the binding energy of a neutron in the 87Kr nucleus. In this case, the 87Kr nucleus can undergo (with the probability of 2.5%) a neutron emission, leading to a stable 87Kr isotope.
According to the JEFF 3.1 database, about 240 n-emitters are known between 8He and 210Tl. About 75 of them are in the non-fission region. Furthermore, experimentally confirmed 18 2n-emitter and only four 3n-emitters ( 11Li, 14Be, 17B, 31Na). These numbers are not certainly final. Since the new IAEA Co-ordinated Research Project (CRP) on Beta-delayed neutron emission evaluation was started in 2013, it is expected these numbers will change significantly.
See also: IAEA, Beta-delayed neutron emission evaluation, INDC(NDS)-0599
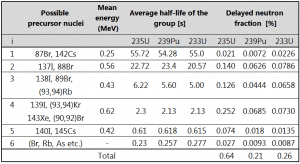
As can be seen, it was identified many precursor nuclei. Not all of them are fission products (about 75 of them in the non-fission region A<70), but many precursor nuclei are in the fission region between A=70-150. Their half-lives range between tenths of second (0.12 s) and tens of seconds (55.6 s). Therefore their delayed neutrons appear with considerably differing delay times.
Six Groups of Delayed Neutrons
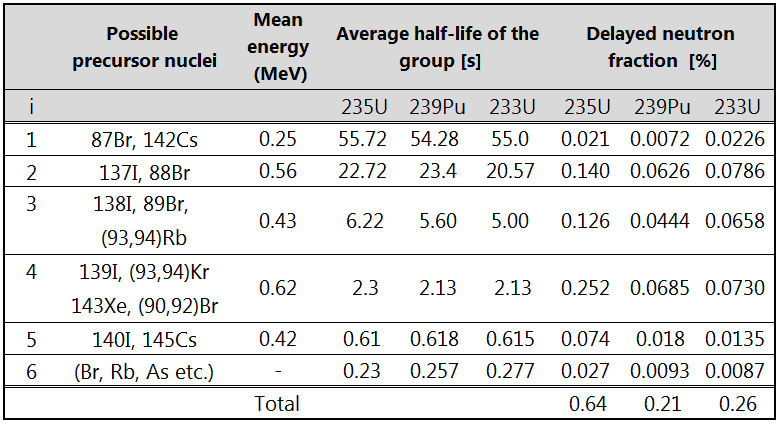
Reactor-kinetic calculations considering such many initial conditions would be correct, but they would also be very complicated. Therefore G. R. Keepin and his co-workers suggested grouping together the precursors based on their half-lives.
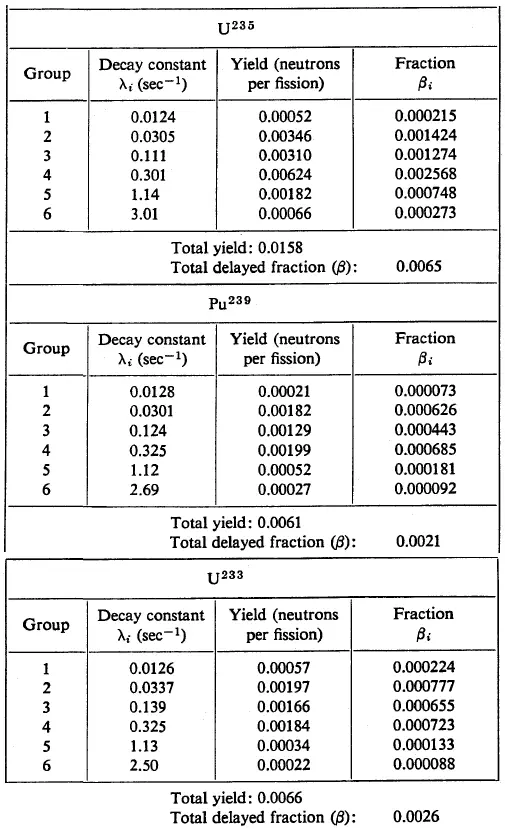
Therefore delayed neutrons are traditionally represented by six delayed neutron groups, whose yields and decay constants (λ) are obtained from nonlinear least-squares fits experimental measurements. This model has the following disadvantages:
- All constants for each group of precursors are empirical fits to the data.
- They cannot be matched with decay constants of specific precursors.
- These constants are different for each fissionable nuclide.
- These constants also change with the neutron energy spectrum.
Although this six-group parameterization still satisfies the requirements of commercial organizations, higher accuracy of the delayed neutron yields and a better energy resolution in the delayed neutron spectra is desired.
It was recognized that the half-lives in the six-group structure do not accurately reproduce the asymptotic die-away time constants associated with the three longest-lived dominant precursors: 87Br, 137I, and 88Br.
This model may be insufficient, especially in the case of epithermal reactors, because virtually all delayed neutron activity measurements have been performed for fast or thermal-neutron-induced fission. In the case of fast reactors, the nuclear fission of six fissionable isotopes of uranium and plutonium is important. The accuracy and energy resolution may play an important role.
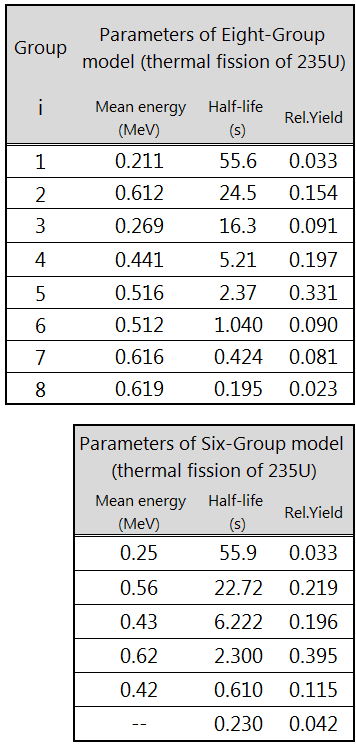
Eight Groups of Delayed Neutrons
To reduce discrepancies between measured and calculated values of the reactivity scale based on reactor kinetics (this discrepancy results in excessive conservatism in the design because uncertainties must cover it during core design and safety analyses calculations), the NEA (Nuclear Energy Agency) and its NEANSC/WPEC Subgroup 6 recommends a new eight-group representation. It seems reasonable to increase the number of delayed neutron groups because many studies have shown that most delayed neutrons are produced approximately by twelve precursors common to all fissioning isotopes.
The eight-group representation uses a set of eight-group half-lives for all fissioning systems, with the half-lives adopted for the three longest-lived groups corresponding to the three dominant long-lived precursors: 87Br, 137I, and 88Br (these precursors was separated into single groups).
See also: Delayed Neutron Data for the Major Actinidies, NEA/WPEC–6. OECD 2002.
Photoneutrons
In nuclear reactors, gamma radiation also plays a significant role in reactor kinetics and subcritical control, especially in nuclear reactors with D2O moderator (CANDU reactors) or Be reflectors (some experimental reactors). Neutrons can also be produced in (γ, n) reactions, and therefore they are usually referred to as photoneutrons.
A high-energy photon (gamma-ray) can, under certain conditions, eject a neutron from a nucleus. It occurs when its energy exceeds the binding energy of the neutron in the nucleus. Most nuclei have binding energies in excess of 6 MeV, above the energy of most gamma rays from fission.
On the other hand, few nuclei with sufficiently low binding energy are of practical interest. These are 2D, 9Be, 6Li, 7Li, and 13C. As can be seen from the table, the lowest threshold have 9Be with 1.666 MeV and 2D with 2.226 MeV.
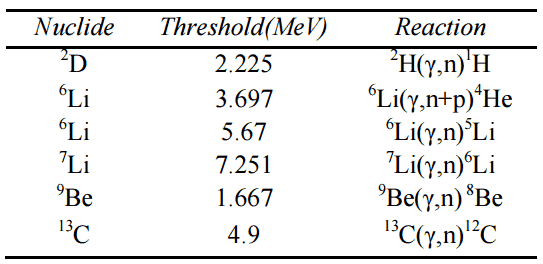
threshold energies.
In the case of deuterium, neutrons can be produced by the interaction of gamma rays (with a minimum energy of 2.22 MeV) with deuterium:
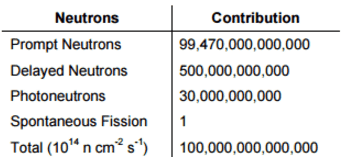
Because fission products with certain delays can emit gamma rays, and the process is very similar to that through which a “true” delayed neutron is emitted, photoneutrons are usually treated no differently than regularly delayed neutrons in the kinetic calculations. Photoneutron precursors can also be grouped by their decay constant, similarly to “real” precursors. The table below shows the relative importance of source neutrons in CANDU reactors by showing the makeup of the full power flux.
Even though photoneutrons are important, especially in CANDU reactors, deuterium nuclei are always present (~0.0156%) in the light water of LWRs. Moreover, the capture of neutrons in the water molecules’ hydrogen nucleus yields small amounts of D2O. This enhances the heavy water concentration. Therefore, in LWRs kinetic calculations, photoneutrons from D2O are treated as additional groups of delayed neutrons with characteristic decay constants λj and effective group fractions.
After a nuclear reactor has been operating at full power for some time, there will be a considerable build-up of gamma rays from the fission products. This high gamma flux from short-lived fission products will decrease rapidly after shutdown. In the long term, the photo neutron source decreases with the decay of long-lived fission products that produce delayed high-energy gamma rays, and the photo neutron source drops slowly, decreasing a little each day. The longest-lived fission product with gamma-ray energy above the threshold is 140Ba with a half-life of 12.75 days.
The amount of fission products present in the fuel elements depends on how long the reactor has been operated before shutdown and at which power level has been operated before shutdown. Photoneutrons are usually a major source in a reactor and ensure sufficient neutron flux on source range detectors when the reactor is subcritical in long-term shutdown.
Compared with fission neutrons, which make a self-sustaining chain reaction possible, delayed neutrons make reactor control possible, and photoneutrons are important at low power operation.
Delayed Neutrons Fraction
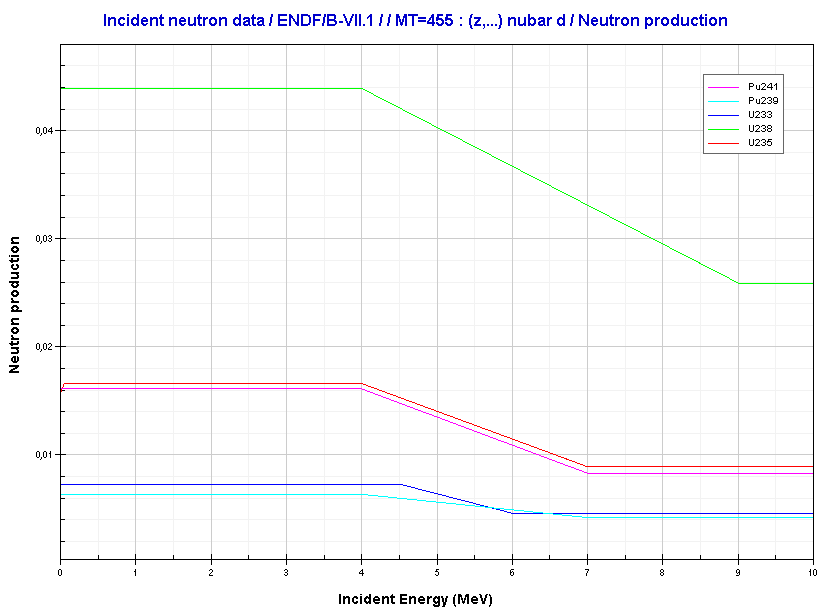
The total yield of delayed neutrons per fission, vd, depends on:
- An isotope that is fissioned (see table).
- The energy of a neutron induces fission (see chart).
In reactor kinetic calculations, it is convenient to use relative units as delayed neutron fraction (DNF). At the steady-state condition of criticality, with keff = 1, the delayed neutron fraction equals the precursor yield fraction (β).
where βi is defined as the fraction of the neutrons which appear as delayed neutrons in the ith group. In contrast to the prompt neutrons emitted with a continuous energy spectrum, the delayed neutrons in each group appear with a more or less well-defined energy. In general, the delayed neutrons are emitted with much less energy than the most prompt neutrons.
The distinction between these two parameters is obvious. The delayed neutron fraction is dependent on the certain reactivity of the multiplying system. On the other hand, β is not dependent on reactivity. These two factors, DNF and β, are not the same things in case of a rapid change in the number of neutrons in the reactor.
In LWRs, the delayed neutron fraction decreases with fuel burnup. This is due to isotopic changes in the fuel. It is simple. Fresh uranium fuel contains only 235U as the fissile material, meanwhile, during fuel burnup, the importance of fission of 239Pu increases (in some cases up to 50%). Since 239Pu produces significantly less delayed neutrons, the resultant core delayed neutron fraction of a multiplying system decreases (the weighted average of the constituent delayed neutron fractions). This is also the reason why the neutron spectrum in the core becomes harder with fuel burnup.
βcore= ∑ Pi.βi
where Pi is a fraction of power generated by isotope i.
Example:
Let say the reactor is at the beginning of the cycle and approximately 98% of reactor power is generated by 235U fission and 2% by 238U fission as a result of fast fission. Calculate the core delayed neutron fraction.
βcore= ∑ Pi.βi = 0.98 x β235 + 0.02 x β238
= 0.98 x 0.0065 + 0.02 x 0.0157
= 0.0064 + 0.0003
= 0.0067
Delayed Neutrons Energy Spectra
The key properties of delayed neutrons, which are very important for the nuclear reactor design, also belong to delayed neutron energy spectra. The energy spectra of the delayed neutrons are the poorest known of all input data required because it is very difficult to measure them.
Depending on the type of the reactor, and their spectrum, the delayed neutrons may be more (in thermal reactors) or less effective than prompt neutrons (in fast reactors). The effectively delayed neutron fraction – βeff must be defined to include this effect into the reactor kinetic calculations.
Effective Delayed Neutron Fraction – βeff
The delayed neutron fraction, β, is the fraction of delayed neutrons in the core at creation at high energies. But in the case of thermal reactors, the fission can be initiated mainly by a thermal neutron. Thermal neutrons are of practical interest in the study of thermal reactor behavior. The effectively delayed neutron fraction usually referred to as βeff, is the same fraction at thermal energies.
The effectively delayed neutron fraction reflects the ability of the reactor to thermalize and utilize each neutron produced. The β is not the same as the βeff due to the fact delayed neutrons do not have the same properties as prompt neutrons released directly from fission. In general, delayed neutrons have lower energies than prompt neutrons. Prompt neutrons have initial energy between 1 MeV and 10 MeV, with an average energy of 2 MeV. Delayed neutrons have initial energy between 0.3 and 0.9 MeV with an average energy of 0.4 MeV.
Therefore, in thermal reactors, a delayed neutron traverses a smaller energy range to become thermal. It is also less likely to be lost by leakage or parasitic absorption than the 2 MeV prompt neutron. On the other hand, delayed neutrons are also less likely to cause fast fission because their average energy is less than the minimum required for fast fission to occur.
These two effects (lower fast fission factor and higher fast non-leakage probability for delayed neutrons) tend to counteract each other and form a term called the importance factor (I). The importance factor relates the average delayed neutron fraction to the effectively delayed neutron fraction. As a result, the effectively delayed neutron fraction is the product of the average delayed neutron fraction and the importance factor.
βeff = β . I
The delayed and prompt neutrons have a difference in their effectiveness in producing a subsequent fission event. Since the energy distribution of the delayed neutrons also differs from group to group, the different groups of delayed neutrons will also have different effects. Moreover, a nuclear reactor contains a mixture of fissionable isotopes. Therefore, the important factor is insufficient in some cases, and an important function must be defined.
For example:
In a small thermal reactor with highly enriched fuel, the increase in fast non-leakage probability will dominate the decrease in the fast fission factor, and the important factor will be greater than one.
In a large thermal reactor with low enriched fuel, the decrease in the fast fission factor will dominate the increase in the fast non-leakage probability, and the important factor will be less than one (about 0.97 for a commercial PWR).

In large fast reactors, the decrease in the fast fission factor will also dominate the increase in the fast non-leakage probability, and the βeff is less than β by about 10%.
Mean Generation Time with Delayed Neutrons
Mean Generation Time with Delayed Neutrons, ld, is the weighted average of the prompt generation times and a delayed neutron generation time. The delayed neutron generation time, τ, is the weighted average of mean precursor lifetimes of the six groups (or more groups) of delayed neutron precursors.
It must be noted, the true lifetime of delayed neutrons (the slowing downtime and the diffusion time) is very short compared with the mean lifetime of their precursors (ts + td << τi). Therefore τi is also equal to the mean lifetime of a neutron from the ith group, that is, τi = li, and the equation for mean generation time with delayed neutrons is the following:
ld = (1 – β).lp + ∑li . βi => ld = (1 – β).lp + ∑τi . βi
where
- (1 – β) is the fraction of all neutrons emitted as prompt neutrons
- lp is the prompt neutron lifetime
- τi is the mean precursor lifetime, the inverse value of the decay constant τi = 1/λi
- The weighted delayed generation time is given by τ = ∑τi . βi / β = 13.05 s
- Therefore the weighted decay constant λ = 1 / τ ≈ 0.08 s-1
The number, 0.08 s-1, is relatively high and has a dominating effect on reactor time response, although delayed neutrons are a small fraction of all neutrons in the core. This is best illustrated by calculating a weighted mean generation time with delayed neutrons:
ld = (1 – β).lp + ∑τi . βi = (1 – 0.0065). 2 x 10-5 + 0.085 = 0.00001987 + 0.085 ≈ 0.085

In short, the mean generation time with delayed neutrons is about ~0.1 s, rather than ~10-5 as in section Prompt Neutron Lifetime, where the delayed neutrons were omitted.
Example – Infinite Multiplying System Without Source and with Delayed Neutrons
The simplest equation governing the neutron kinetics of the system with delayed neutrons is the point kinetics equation. This equation states that the time change of the neutron population is equal to the excess of neutron production (by fission) minus neutron loss by absorption in one mean generation time with delayed neutrons (ld). The role of ld is evident. Longer lifetimes give simply slower responses to multiplying systems.
If there are neutrons in the system at t=0, that is, if n(0) > 0, the solution of this equation gives the simplest point kinetics equation with delayed neutrons (similarly to the case without delayed neutrons):
Let us consider that the mean generation time with delayed neutrons is ~0.085, and k (k∞ – neutron multiplication factor) will increase by only 0.01% (i.e., 10 pcm or ~1.5 cents), k∞=1.0000 will increase to k∞=1.0001.
It must be noted such reactivity insertion (10pcm) is very small in the case of LWRs. The reactivity insertions of the order of one pcm are for LWRs practically unrealizable. In this case, the reactor period will be:
T = ld / (k∞-1) = 0.085 / (1.0001-1) = 850s
This is a very long period. In ~14 minutes, the reactor’s neutron flux (and power) would increase by a factor of e = 2.718. This is a completely different dimension of the response on reactivity insertion compared to the case without delayed neutrons, where the reactor period was 1 second.
Reactors with such kinetics would be quite easy to control. From this point of view, it may seem that reactor control will be quite a boring affair. It will not! The presence of delayed neutrons entails many, many specific phenomena that will be described in later chapters.
Interactive chart – Infinite Multiplying System Without Source and Delayed Neutrons
Press the “clear and run” button and try to increase the power of the reactor.
Compare the response of the reactor with the case of Infinite Multiplying System Without Source and without Delayed Neutrons (or set the β = 0).
Effective Precursor Decay Constant – Lambda-Effective
The effectively delayed neutron precursor decay constant (pronounced lambda effective) is a new term, which has to be introduced in the reactor period equation in the case of a single precursor group model. Creating a simple kinetic model conducive to understanding reactor behavior is useful to further reduce the precursors to a single group. But if we do this, the convention is to employ a constant precursor yield fraction and a variable precursor decay rate, as defined by lambda effective (λeff). In the single precursor group model, the lambda effect is not a constant but rather a dynamic property that depends on the mix of precursor atoms resulting from the reactivity.
The reason the constant decay constant cannot be used is as follows. There is a difference in the decay and the creation of short-lived and long-lived precursors during power transients.
During a power increase (positive reactivity), the short-lived precursors decaying at any given instant were born at a higher power level than the longer-lived precursors decaying at the same instant. The short-lived precursors become more significant. As the magnitude of the positive reactivity increases, the value of lambda effective increases closer to that of the short-lived precursors (let say 0.1 s-1 for +100pcm).
During a power decrease (negative reactivity), the long-lived precursors decaying at a given instant were born at a higher power level than the short-lived precursors decaying at that instant. The long-lived precursors become more significant. As the magnitude of the negative reactivity increases, the value of lambda effective decreases closer to that of the long-lived precursors (let say 0.05 s-1 for -100pcm).
If the reactor operates at a steady-state operation, all the precursor groups reach an equilibrium value, and the λeff value is approximately 0.08 s-1.
Effect of Delayed Neutrons on Reactor Control
Despite the fact, the number of delayed neutrons per fission neutron is quite small (typically below 1%) and thus does not contribute significantly to the power generation, they play a crucial role in the reactor control and are essential from the point of view of reactor kinetics and reactor safety. Their presence completely changes the dynamic time response of a reactor to some reactivity change, making it controllable by control systems such as the control rods.
Delayed neutrons allow to operate a reactor in a prompt subcritical, delayed critical condition. All power reactors are designed to operate in delayed critical conditions and are provided with safety systems to prevent them from ever achieving prompt criticality.
For typical PWRs, the prompt criticality occurs after positive reactivity insertion of βeff (i.e., keff ≈ 1.006 or ρ = +600 pcm). In power reactors, such a reactivity insertion is practically impossible to insert (in case of normal and abnormal operation), especially when a reactor is in power operation mode and a reactivity insertion causes heating of a reactor core. Due to the presence of reactivity feedbacks, the positive reactivity insertion is counterbalanced by the negative reactivity from moderator and fuel temperature coefficients. The presence of delayed neutrons is also of importance from this point of view because they also provide time for reactivity feedback to react on undesirable reactivity insertion.