Facebook Instagram Youtube Twitter

Infinite Multiplying System Without Source and with Delayed Neutrons

Example – Infinite Multiplying System Without Source and Delayed Neutrons

The simplest equation governing the neutron kinetics of the system with delayed neutrons is the point kinetics equation. This equation states that the time change of the neutron population is equal to the excess of neutron production (by fission) minus neutron loss by absorption in one mean generation time with delayed neutrons (ld). The role of ld is evident. Longer lifetimes give simply slower responses to multiplying systems.

If there are neutrons in the system at t=0, that is, if n(0) > 0, the solution of this equation gives the simplest point kinetics equation with delayed neutrons (similarly to the case without delayed neutrons):point kinetics equation with delayed neutrons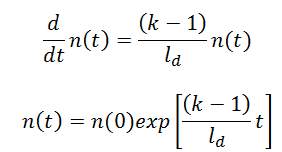Let us consider that the mean generation time with delayed neutrons is ~0.085 and k (k∞ – neutron multiplication factor) will be step increased by only 0.01% (i.e., 10pcm or ~1.5 cents), that is k∞=1.0000 will increase to k∞=1.0001.

It must be noted such reactivity insertion (10pcm) is very small in the case of LWRs. The reactivity insertions of the order of one pcm are for LWRs practically unrealizable. In this case, the reactor period will be:

T = ld / (k∞-1) = 0.085 / (1.0001-1) = 850s

This is a very long period. In ~14 minutes, the reactor’s neutron flux (and power) would increase by a factor of e = 2.718. This is a completely different dimension of the response on reactivity insertion compared to the case without delayed neutrons, where the reactor period was 1 second.

Reactors with such kinetics would be quite easy to control. From this point of view, it may seem that reactor control will be quite a boring affair. It will not! The presence of delayed neutrons entails many, many specific phenomena that will be described in later chapters.

Interactive chart – Infinite Multiplying System Without Source and with Delayed Neutrons

Press the “clear and run” button and try to increase the power of the reactor.

Compare the response of the reactor with the case of Infinite Multiplying System Without Source and without Delayed Neutrons (or set the β = 0).

 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2. 
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See previous:

Mean Generation Time

See above:

Delayed Neutrons

See next:

Lambda-Effective