Facebook Instagram Youtube Twitter

Key Characteristics of Delayed Neutrons

Key Characteristics of Delayed Neutrons

  • The presence of delayed neutrons is perhaps the most important aspect of the fission process from reactor control.
  • Delayed neutrons are emitted by neutron-rich fission fragments that are called delayed neutron precursors.
  • These precursors usually undergo beta decay, but a small fraction of them are excited enough to undergo neutron emission.
  • The emission of neutrons happens orders of magnitude later compared to the emission of the prompt neutrons.
  • About 240 n-emitters are known between 8He and 210Tl. About 75 of them are in the non-fission region.
  • It is suggested to group together the precursors based on their half-lives to simplify reactor kinetic calculations.
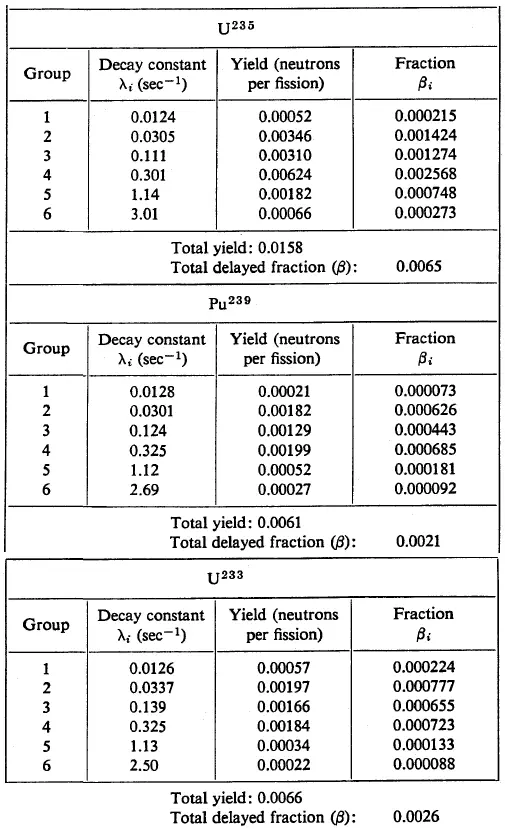
  • Therefore delayed six delayed neutron groups traditionally represent neutrons.
  • Neutrons can also be produced in (γ, n) reactions (especially in reactors with heavy water moderators), and therefore, they are usually referred to as photoneutrons. Photoneutrons are usually treated no differently than regularly delayed neutrons in the kinetic calculations.
  • The total yield of delayed neutrons per fission, vd, depends on:
    • An isotope that is fissioned.
    • The energy of a neutron induces fission.
  • Variation among individual group yields is much greater than variation among group periods.
  • In reactor kinetic calculations, it is convenient to use relative units usually referred to as delayed neutron fraction (DNF).
  • At the steady-state condition of criticality, with keff = 1, the delayed neutron fraction is equal to the precursor yield fraction β.
  • In LWRs, the β decreases with fuel burnup. This is due to isotopic changes in the fuel.
  • Delayed neutrons have initial energy between 0.3 and 0.9 MeV with an average energy of 0.4 MeV.
  • Depending on the type of the reactor, and their spectrum, the delayed neutrons may be more (in thermal reactors) or less effective than prompt neutrons (in fast reactors). The effectively delayed neutron fraction – βeff must be defined to include this effect in the reactor kinetic calculations.
  • The effectively delayed neutron fraction is the product of the average delayed neutron fraction and the importance factor βeff = β . I.
  • The weighted delayed generation time is given by τ = ∑iτi . βi / β = 13.05 s, therefore the weighted decay constant λ = 1 / τ ≈ 0.08 s-1.
  • The mean generation time with delayed neutrons is about ~0.1 s, rather than ~10-5 as in section Prompt Neutron Lifetime, where the delayed neutrons were omitted.
  • Their presence completely changes the dynamic time response of a reactor to some reactivity change, making it controllable by control systems such as the control rods.
Table of main kinetic parameters.

Table of main kinetic parameters.

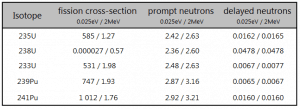
Table of key prompt and delayed neutrons characteristics
Table of key prompt and delayed neutrons characteristics. Thermal vs. Fast Fission
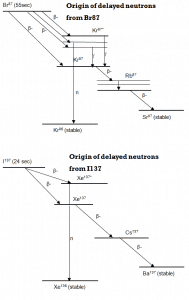
Precursors of Delayed Neutrons
Precursors of Delayed Neutrons

Delayed neutron fraction - yield

Source: Keepin, G. R., Physics of Nuclear Kinetics. Addison-Wesley, 1965.
Delayed Neutron Production
This chart shows the energy dependency of delayed neutrons production. The delayed neutrons production remains constant to 4 MeV, then a linear decrease is observed. Source: JANIS (Java-based Nuclear Data Information Software); ENDF/B-VII.1
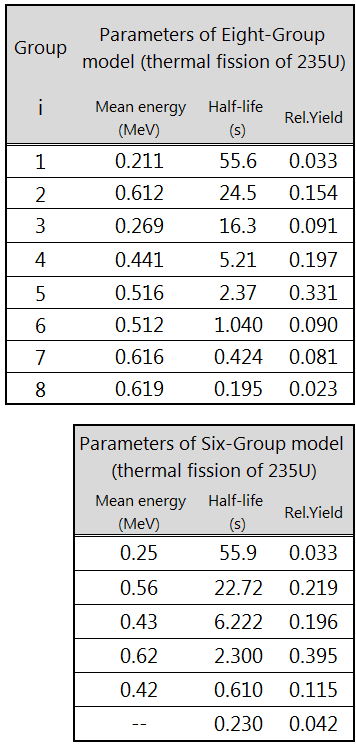Delayed Neutrons - Eight Groups
Delayed neutrons are traditionally represented by six delayed neutron groups, but a new eight-group representation is recommended.Source: DELAYED NEUTRON DATA FOR THE MAJOR ACTINIDES, NEA/WPEC–6. Subgroup 6, NEA.https://www.oecd-nea.org/science/wpec/volume6/volume6.pdf

Example – Infinite Multiplying System Without Source and Delayed Neutrons

The simplest equation governing the neutron kinetics of the system with delayed neutrons is the point kinetics equation. This equation states that the time change of the neutron population is equal to the excess of neutron production (by fission) minus neutron loss by absorption in one mean generation time with delayed neutrons (ld). The role of ld is evident. Longer lifetimes give simply slower responses to multiplying systems.

If there are neutrons in the system at t=0, that is, if n(0) > 0, the solution of this equation gives the simplest point kinetics equation with delayed neutrons (similarly to the case without delayed neutrons):point kinetics equation with delayed neutrons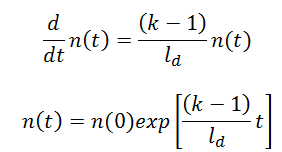Let us consider that the mean generation time with delayed neutrons is ~0.085 and k (k∞ – neutron multiplication factor) will be step increased by only 0.01% (i.e., 10pcm or ~1.5 cents), that is k∞=1.0000 will increase to k∞=1.0001.

It must be noted such reactivity insertion (10pcm) is very small in the case of LWRs. The reactivity insertions of the order of one pcm are for LWRs practically unrealizable. In this case, the reactor period will be:

T = ld / (k∞-1) = 0.085 / (1.0001-1) = 850s

This is a very long period. In ~14 minutes, the reactor’s neutron flux (and power) would increase by a factor of e = 2.718. This is a completely different dimension of the response on reactivity insertion compared to the case without delayed neutrons, where the reactor period was 1 second.

Reactors with such kinetics would be quite easy to control. From this point of view, it may seem that reactor control will be quite a boring affair. It will not! The presence of delayed neutrons entails many, many specific phenomena that will be described in later chapters.

Interactive chart – Infinite Multiplying System Without Source and with Delayed Neutrons

Press the “clear and run” button and try to increase the power of the reactor.

Compare the response of the reactor with the case of Infinite Multiplying System Without Source and without Delayed Neutrons (or set the β = 0).

 
References:
Nuclear and Reactor Physics:
  1. J. R. Lamarsh, Introduction to Nuclear Reactor Theory, 2nd ed., Addison-Wesley, Reading, MA (1983).
  2. J. R. Lamarsh, A. J. Baratta, Introduction to Nuclear Engineering, 3d ed., Prentice-Hall, 2001, ISBN: 0-201-82498-1.
  3. W. M. Stacey, Nuclear Reactor Physics, John Wiley & Sons, 2001, ISBN: 0- 471-39127-1.
  4. Glasstone, Sesonske. Nuclear Reactor Engineering: Reactor Systems Engineering, Springer; 4th edition, 1994, ISBN: 978-0412985317
  5. W.S.C. Williams. Nuclear and Particle Physics. Clarendon Press; 1 edition, 1991, ISBN: 978-0198520467
  6. G.R.Keepin. Physics of Nuclear Kinetics. Addison-Wesley Pub. Co; 1st edition, 1965
  7. Robert Reed Burn, Introduction to Nuclear Reactor Operation, 1988.
  8. U.S. Department of Energy, Nuclear Physics and Reactor Theory. DOE Fundamentals Handbook, Volume 1 and 2. January 1993.

Advanced Reactor Physics:

  1. K. O. Ott, W. A. Bezella, Introductory Nuclear Reactor Statics, American Nuclear Society, Revised edition (1989), 1989, ISBN: 0-894-48033-2.
  2. K. O. Ott, R. J. Neuhold, Introductory Nuclear Reactor Dynamics, American Nuclear Society, 1985, ISBN: 0-894-48029-4.
  3. D. L. Hetrick, Dynamics of Nuclear Reactors, American Nuclear Society, 1993, ISBN: 0-894-48453-2. 
  4. E. E. Lewis, W. F. Miller, Computational Methods of Neutron Transport, American Nuclear Society, 1993, ISBN: 0-894-48452-4.

See previous:

Description of Delayed Neutrons

See above:

Delayed Neutrons

See next:

Precursors of Delayed Neutrons