Facebook Instagram Youtube Twitter

Liquid Drop Model of Nucleus

Article Summary & FAQs

What is liquid drop model of nucleus?

In nuclear physics, the liquid drop model of the nucleus describes forces in atomic nuclei as if a tiny liquid drop formed the atomic nucleus. But in this nuclear scale, the fluid is made of nucleons (protons and neutrons). The liquid drop model considers that the forces on the nucleons on the surface are different from those on nucleons on the interior, where other attracting nucleons completely surround them. This is similar to taking into account surface tension as a contributor to the energy of a tiny liquid drop.

Key Facts

  • Scattering experiments suggest that nuclei have approximately constant density.
  • Nuclei have their volume and surface, where forces act differently.
  • In the ground state, the nucleus is spherical.
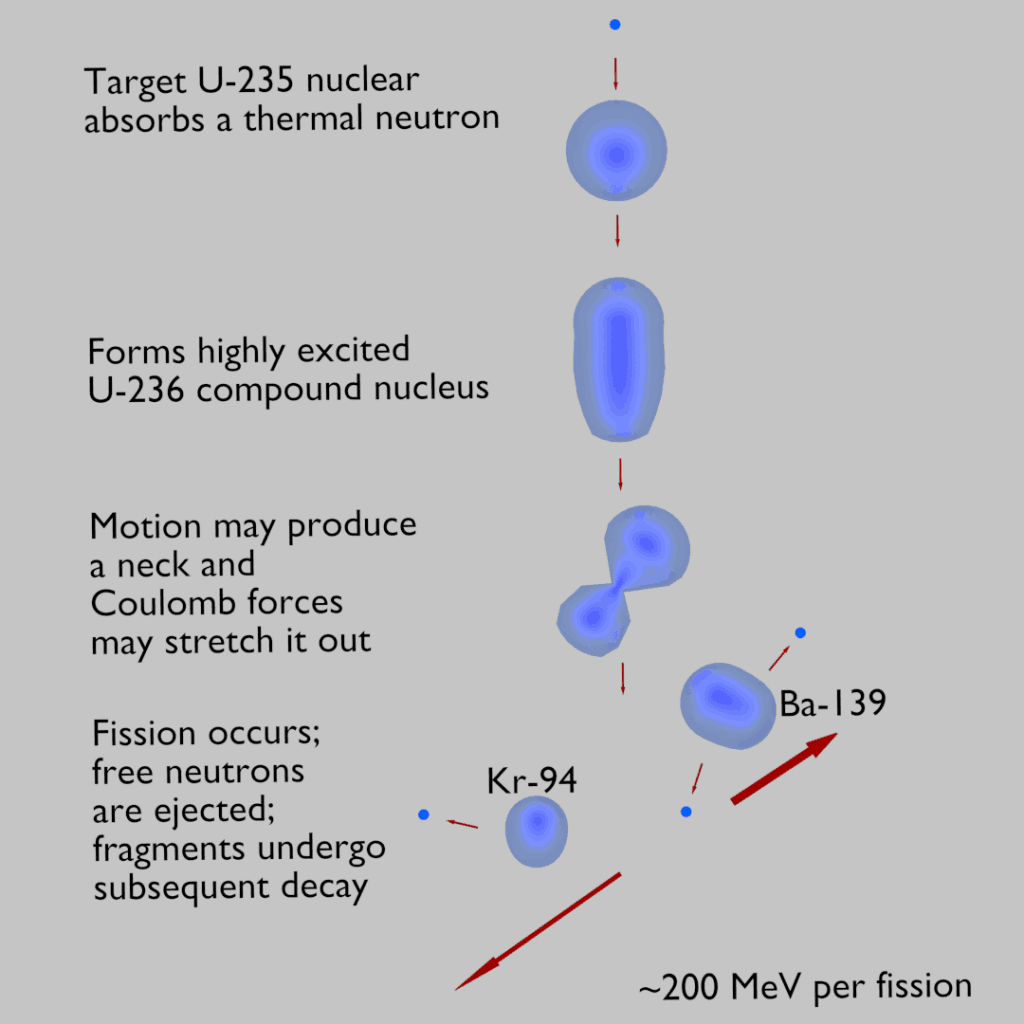
  • If sufficient kinetic or binding energy is added, this spherical nucleus may be distorted into a dumbbell shape and then maybe split into two fragments.
  • The Weizsaecker formula is an empirically refined form of the liquid drop model for the binding energy of nuclei. It has the following terms:
    • Volume term
    • Surface term
    • Asymmetry term
    • Pairing term
  • Using the Weizsaecker formula, the binding energies and also masses of atomic nuclei can be derived. Therefore, we can also derive the energy released per fission.
What is the Weizsaecker formula?
What is the Weizsaecker formula?

One of the first models that could describe the behavior of the nuclear binding energies and therefore of nuclear masses was the mass formula of von Weizsaecker (also called the semi-empirical mass formula – SEMF) published in 1935 by German physicist Carl Friedrich von Weizsäcker. This theory is based on the liquid drop model proposed by George Gamow.

What are the terms of the Weizsaecker formula?
What are the terms of the Weizsaecker formula?

The Weizsaecker formula has the following terms:

  • Volume term
  • Surface term
  • Asymmetry term
  • Pairing term
What is the use of liquid drop model?
What is the use of the liquid drop model?

Using the Weizsaecker formula, the binding energies and also masses of atomic nuclei can be derived. Therefore, we can also derive the energy released per fission. According to the Weizsaecker formula, the total energy released for such a reaction will be approximately 235 x (8.5 – 7.6) ≈ 200 MeV.

Liquid Drop Model of Nucleus

Liquid Drop ModelOne of the first models that could describe the behavior of the nuclear binding energies and therefore of nuclear masses was the mass formula of von Weizsaecker (also called the semi-empirical mass formula – SEMF) published in 1935 by German physicist Carl Friedrich von Weizsäcker. This theory is based on the liquid drop model proposed by George Gamow.

According to this model, the atomic nucleus behaves like the molecules in a drop of liquid. But in this nuclear scale, the fluid is made of nucleons (protons and neutrons), held together by the strong nuclear force. The liquid drop model of the nucleus considers that the nuclear forces on the nucleons on the surface are different from those on nucleons in the interior of the nucleus. Other attractive nucleons completely surround the interior nucleons. Here is the analogy with the forces that form a drop of liquid.

In the ground state, the nucleus is spherical. If sufficient kinetic or binding energy is added, this spherical nucleus may be distorted into a dumbbell shape and then maybe split into two fragments. Since these fragments are more stable, the splitting of such heavy nuclei must be accompanied by energy release. This model does not explain all the properties of the atomic nucleus but does explain the predicted nuclear binding energies.

The nuclear binding energy as a function of the mass number A and the number of protons Z based on the liquid drop model can be written as: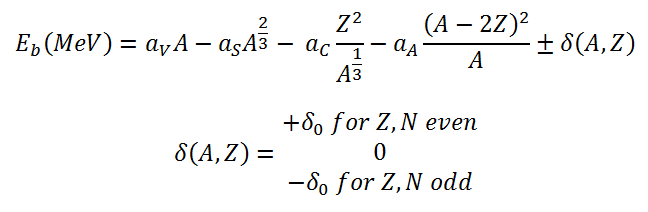Weizsaecker formula - semi-empirical mass formulaThis formula is called the Weizsaecker Formula (or the semi-empirical mass formula). The physical meaning of this equation can be discussed term by term.

 
Volume term
Volume term – aV.A. The first two terms describe a spherical liquid drop of an incompressible fluid that contributes from the volume scaling with A and from the surface, scaling with A2/3. The first positive term, aV.A is known as the volume term, which is caused by attracting strong forces between the nucleons. The strong force has a very limited range, and a given nucleon may only interact with its direct neighbors. Therefore this term is proportional to A instead of A2. The coefficient aV is usually about ~ 16 MeV.
Surface term
Surface term – asf.A2/3. The surface term is also based on the strong force. It is, in fact, a correction to the volume term. The point is that other particles do not surround particles at the surface of the nucleus. In the volume term, it is suggested that each nucleon interacts with a constant number of nucleons, independent of A. This assumption is nearly true for nucleons deep within the nucleus but causes an overestimation of the binding energy on the surface. By analogy with a liquid drop, this effect is indicated as the surface tension effect. If the volume of the nucleus is proportional to A, then the geometrical radius should be proportional to A1/3, the surface term must be proportional to the surface area, i.e., proportional to A2/3.
Coulomb term
Coulomb term – aC.Z2.A-⅓. This term describes the Coulomb repulsion between the uniformly distributed protons and is proportional to the number of proton pairs Z2/R, whereby R is proportional to A1/3. This effect lowers the binding energy because of the repulsion between charges of the equal sign.
Asymmetry term
Asymmetry term – aA.(A-2Z)2/A. This term cannot be described as ‘classically’ as the first three. This effect is not based on any of the fundamental forces, and this effect is based only on the Pauli exclusion principle (no two fermions can occupy the same quantum state in an atom). The heavier nuclei contain more neutrons than protons. These extra neutrons are necessary for the stability of the heavier nuclei. They provide (via the attractive forces between the neutrons and protons) some compensation for the repulsion between the protons. On the other hand, if there are significantly more neutrons than protons in a nucleus, some of the neutrons will be higher in energy levels in the nucleus. This is the basis for a correction factor, the so-called symmetry term.
Pairing term
Pairing term – δ(A,Z). The last term is the pairing term δ(A, Z). This term captures the effect of spin-coupling. Nuclei with an even number of protons and an even number of neutrons are (due to the Pauli exclusion principle) very stable thanks to the occurrence of ‘paired spin’. On the other hand, nuclei with an odd number of protons and neutrons are mostly unstable.
Nuclear binding energy curve.
Nuclear binding energy curve.
Source: hyperphysics.phy-astr.gsu.edu

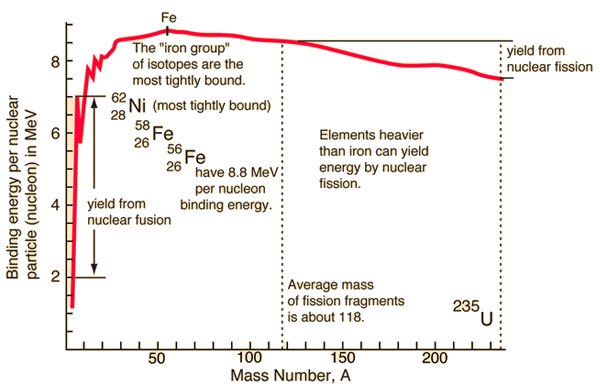
With the aid of the Weizsaecker formula, the binding energy can be calculated very well for nearly all isotopes. This formula provides a good fit for heavier nuclei. For light nuclei, especially for 4He, it provides a poor fit. The main reason is the formula does not consider the internal shell structure of the nucleus.

The coefficients aV, aS, aC, aA, and aP must be known to calculate the binding energy. The coefficients have units of megaelectronvolts (MeV) and are calculated by fitting to experimentally measured masses of nuclei. They usually vary depending on the fitting methodology. According to ROHLF, J. W., Modern Physics from α to Z0, Wiley, 1994., the coefficients in the equation are the following: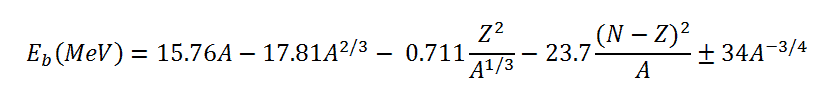Weizsaecker formula - semi-empirical mass formulaUsing the Weizsaecker formula. Also, the mass of an atomic nucleus can be derived and is given by:

m = Z.mp +N.mn -Eb/c2

where mp and mn are the rest mass of a proton and a neutron, respectively, and Eb is the nuclear binding energy of the nucleus. From the nuclear binding energy curve and the table, it can be seen that, in the case of splitting a 235U nucleus into two parts, the binding energy of the fragments (A ≈ 120) together is larger than that of the original 235U nucleus.

According to the Weizsaecker formula, the total energy released for such reaction will be approximately 235 x (8.5 – 7.6) ≈ 200 MeV.

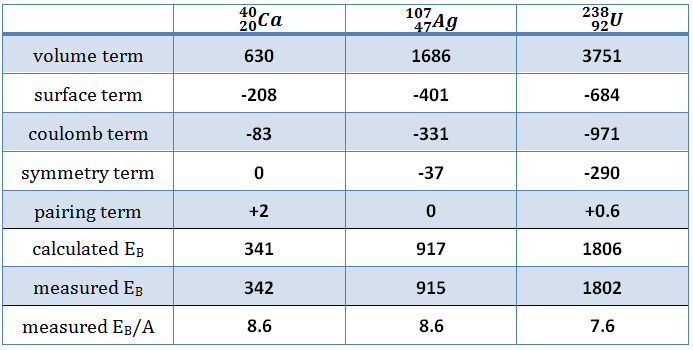the semi-empirical mass formula - weizsaecker formula
Table of binding energies fo some nuclides. Calculated according to the semi-empirical mass formula.
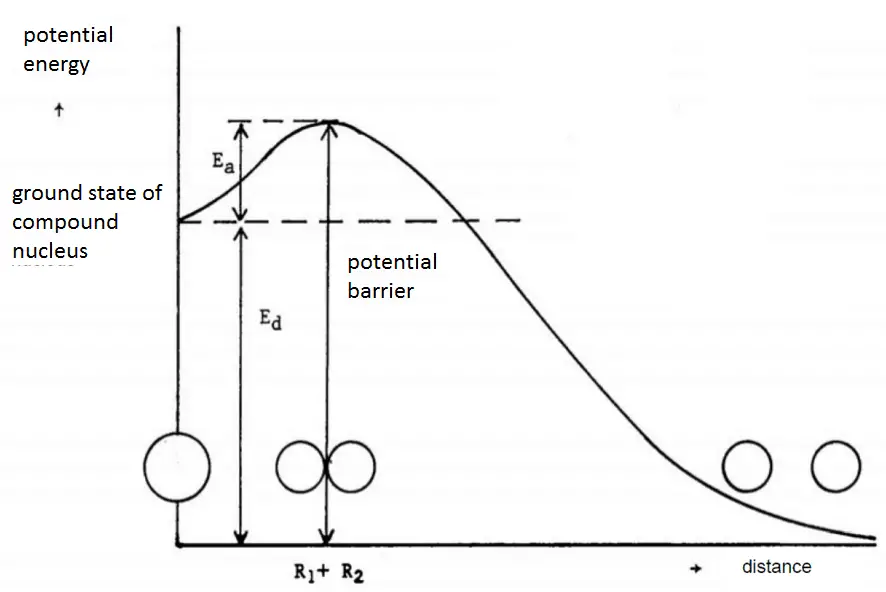Critical Energy - Threshold Energy
The minimum excitation energy required for fission to occur is known as the critical energy (Ecrit) or threshold energy.
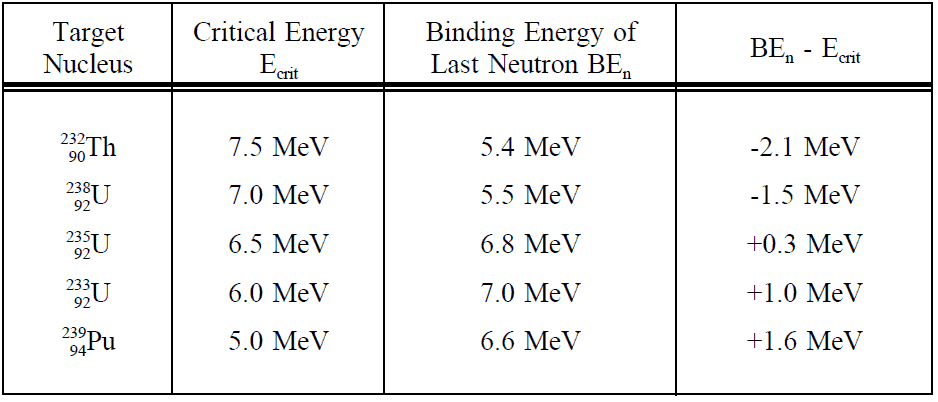Critical Energy to Binding Energy
This table shows critical energies compared to binding energies of the last neutron of a number of nuclei.

See previous:

Binding Energy

See above:

Nuclear Fission

See next:

Critical Energy